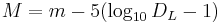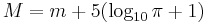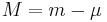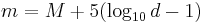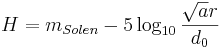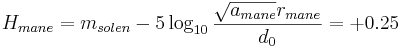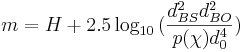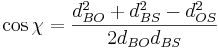Absolut magnitud
Från Rilpedia
Absolut magnitud är inom astronomi den skenbara magnitud, m, ett objekt skulle ha om det var på ett standardavstånd (vanligen 10 parsec) från oss, vid frånvaro av interstellär extinktion. Med hjälp av absolut magnitud kan man jämföra ljusstyrkan hos objekt med olika avstånd från observatören.
Den absoluta magnituden använder samma princip som den skenbara magnituden och har därmed en skillnad i ljusstyrka på ~2,512 mellan stegen, att man har just den siffran beror på att man vill att fem steg ska motsvara en faktor på 100 i ljusstyrka (2,5125 ≈ 100). Vintergatan, till exempel, har en absolut magnitud på ungefär -20,5. Så en kvasar med en absolut magnitud på -25,5 är 100 gånger ljusstarkare än vår galax. Om den här kvasaren och Vintergatan kunde ses sida vid sida skulle kvasaren vara 5 magnituder (eller 100 gånger) ljusstarkare än vår galax.
Innehåll |
Absolut magnitud för stjärnor och galaxer (M)
Inom stjärn- och galaxastronomi är standardavståndet 10 parsec (ungefär 32,616 ljusår, eller 3×1014 kilometer). En stjärna vid 10 parsecs avstånd har en parallax på 0,1" (bågsekunder).
Vid definitionen av absolut magnitud är det nödvändigt att specifiera typen av elektromagnetisk strålning som man mäter. När man syftar på det totala energiflödet är den korrekta termen bolometrisk magnitud. Ju svagare ett objekt (vid ett avstånd på 10 parsec) skulle se ut, desto högre är dess absoluta magnitud. På samma sätt är ett objekt ljusare ju lägre absolut magnitud det har. En matematisk ekvation relaterar skenbar magnitud med absolut magnitud via parallax.
Många stjärnor synliga för det blotta ögat har en absolut magnitud som är kapabel att skapa skuggor från 10 parsec; Rigel (-7,0), Deneb (-7,2), Naos (-6,0), and Betelgeuse (-5,6). Som jämförelse har Sirius en absolut magnitud på 1,4 och solen har en absolut magnitud på 4,83 (och tjänar som en referenspunkt).
Absoluta magnituder hos stjärnor ligger oftast inom intervallet från -10 till +17. Den absoluta magnituden hos galaxer kan vara mycket lägre (ljusare). Till exempel har den enorma elliptiska galaxen M87 en absolut magnitud på -22 och är därmed ca 54 miljarder gånger ljusstarkare än solen (2,51226,83 ≈ 54 × 109)
Beräkning
Den absoluta magnituden 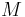 hos ett objekt med en skenbar magnitud på
hos ett objekt med en skenbar magnitud på 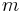 kan beräknas med:
kan beräknas med:
där 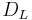 är objektets luminositetsavstånd mätt i parsec (vilket är cirka 3,2616 ljusår).
är objektets luminositetsavstånd mätt i parsec (vilket är cirka 3,2616 ljusår).
För objekt i vår astronomiska närhet (som stjärnor i Vintergatan) är luminositetsavståndet DL nästan identiskt med det riktiga avståndet eftersom rumtiden i vår galax nästan är euklidisk. För objekt mycket längre bort är inte den euklidiska approximationen längre giltig och allmänna relativitetsteorin måste användas för att beräkna ljusstyrkeavståndet för ett sådant objekt.
Med den euklediska approximationen för näraliggande objekt kan den absoluta magnituden 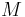 beräknas från dess skenbara magnitud och parallax:
beräknas från dess skenbara magnitud och parallax:
där π är stjärnans parallax i (bågsekunder).
Det går också att beräkna den absoluta magnituden 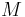 hos ett objekt med den skenbara magnitud
hos ett objekt med den skenbara magnitud 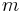 och en avståndsmodul
och en avståndsmodul 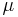 :
:
Exempel
- Rigel har en skenbar magnitud på mV=0,18 och ett avstånd på ungefär 773 ljusår.
- MVRigel = 0,18 + 5*log10(32,616/773) = -6,7
- Vega har en parallax på 0,133" och en skenbar magnitud på +0,03
- MVVega = 0,03 + 5*(1 + log10(0,133)) = +0,65
- Alpha Centauri har en parallax på 0,750" och en skenbar magnitud på -0,01
- MVα Cen = -0,01 + 5*(1 + log10(0,750)) = +4,37
- Galaxen M64 har en skenbar magnitud på mV=+9,36 och en distansmodul på 31,06.
- MVM64y = 9.36 - 31,06 = -20.01
Skenbar magnitud
Med hjälp av den absoluta magnituden 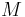 kan du för objekt inom vår galax också räkna ut den skenbara magnituden
kan du för objekt inom vår galax också räkna ut den skenbara magnituden 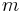 från ett godtyckligt avstånd
från ett godtyckligt avstånd 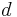 :
:
För objekt på mycket långa avstånd (utanför vår galax) bör luminositetsavståndet DL användas istället för d.
Absolut magnitud hos planeter (H)
För planeter, kometer och asteroider används en annan definition på absolut magnitud som är vettigare för icke stellära objekt.
I det här fallet är den absoluta magnituden definierad som den skenbara magnituden objektet skulle ha om det var en astronomisk enhet (AE) från både observatören och solen samt vid en fasvinkel på 0 grader. Detta är en fysisk omöjlighet eftersom observatören skulle behöva befinna sig i solens centrum, men det är praktiskt för beräkningar och jämförelser.
För att omvandla en stellär eller galaktisk absolut magnitud till en planetär absolut magnitud; subtrahera 31,57. Den här faktorn motsvarar också skillnaden mellan solens skenbara magnitud på -26,8 och dess (stellära) absoluta magnitud på +4,8. Därmed har Vintergatan (med en galaktisk absolut magnitud på -20,5) en planetär absolut magnitud på -52.
Beräkningar
Formel för H: (Absolut magnitud)
där 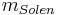 är den skenbara magnituden av solen på ett avstånd av 1 AE (-26.8),
är den skenbara magnituden av solen på ett avstånd av 1 AE (-26.8), 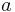 är det geometriska albedo hos objektet (ett värde mellan 0 och 1),
är det geometriska albedo hos objektet (ett värde mellan 0 och 1), 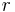 är dess radie och
är dess radie och 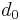 är 1 AE (≈149.6 Gm).
är 1 AE (≈149.6 Gm).
Exempel
Månen: 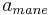 = 0.12,
= 0.12, 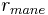 = 3476/2 km = 1738 km
= 3476/2 km = 1738 km
Skenbar magnitud
Den absoluta magnituden kan användas för att beräkna den skenbara magnituden hos ett objekt under vissa förutsättningar.
där
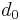 är 1 AE,
är 1 AE, 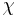 är fasvinkeln, vinkeln mellan sol-objektlinjen och objekt-observatörlinjen. Genom cosinussatsen får vi:
är fasvinkeln, vinkeln mellan sol-objektlinjen och objekt-observatörlinjen. Genom cosinussatsen får vi:
 är fasintegralen (integration av reflekterat ljus, ett värde mellan 0 och 1).
är fasintegralen (integration av reflekterat ljus, ett värde mellan 0 och 1).
Exempel: En ideal diffus reflekterande sfär – en rimlig första approximation för planetära objekt.
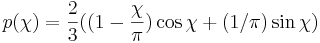
- En fullfas diffus sfär reflekterar ⅔ så mycket ljus som en diffus skiva av samma diameter.
- Avstånd:
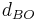 är avståndet mellan observatören och objektet (body).
är avståndet mellan observatören och objektet (body).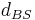 är avståndet mellan solen och objektet.
är avståndet mellan solen och objektet.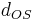 är avståndet mellan observatören och solen.
är avståndet mellan observatören och solen.
Exempel
Månen
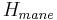 = +0.25
= +0.25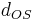 =
= 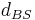 = 1 AE
= 1 AE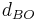 = 384.5 Mm = 2.57 mAE
= 384.5 Mm = 2.57 mAE
- Hur ljus är månen från jorden?
- Fullmåne:
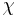 = 0, (
= 0, ( ≈ 2/3)
≈ 2/3)
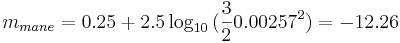
- (Faktiskt värde -12.7) En fullmåne reflekterar 30 % mer ljus vid full fas än en perfekt diffus reflektor förutspår.
- Kvartsmåne:
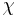 = 90°,
= 90°, 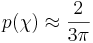 (om diffus reflektor)
(om diffus reflektor)
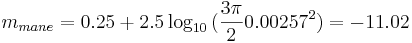
- (Faktiskt värde -11.0) Den diffusa reflektorn fungerar bättre som approximation vid små faser.
- Fullmåne: