Perfekt tal
Från Rilpedia
Inom talteorin är ett perfekt tal ett heltal n för vilket summan av alla sina delare, inklusive n självt, är lika med 2n.
Detta medför att man enkelt kan exkludera n som delare, då summan av delarna är skall vara lika med n. Dock är detta endast en simplifiering.
Innehåll |
Definition
Om ett tal p är ett perfekt tal gäller följande:
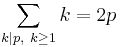
Exempel
6 är ett perfekt tal eftersom det är jämnt delbart med 1, 2 och 3 och summan av dessa är just 6.
De tio första perfekta talen är (talföljd A000396 i OEIS):
- 6 = 1 + 2 + 3
- 28 = 1 + 2 + 4 + 7 + 14
- 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
- 8 128
- 33 550 336
- 8 589 869 056
- 137 438 691 328
- 2 305 843 008 139 952 128
- 2 658 455 991 569 831 744 654 692 615 953 842 176
- 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216
Som framgår ovan växer följden av perfekta tal mycket snabbt. De förekommer alltså väldigt glest bland mängden av tal. År 2001 var endast 39 perfekta tal kända, där det största har över 8 miljoner siffror. Sju år senare, 2008, har antalet kända perfekta tal vuxit till 46. Det är dock inte känt om det finns några perfekta tal som är större än det 39:e, men mindre än det största perfekta tal man hittat, så de senare talens plats är inte definitiva.
Jämna perfekta tal
Alla perfekta tal man känner till är jämna. Euklides bevisade att om 2n - 1 är ett primtal, så är 2n-1(2n - 1) ett perfekt tal. Två tusen år senare bevisade Euler att dessa är de enda jämna perfekta tal som existerar.
Primtal på formen 2n - 1 kallas Mersenneprimtal, så varje Mersenneprimtal man upptäcker ger oss omedelbart ett nytt perfekt tal.
Udda perfekta tal
En hittills obesvarad fråga är om det existerar några udda perfekta tal. Man vet att om det finns sådana, så har de bland annat följande egenskaper:
- är större än 10500
- har minst 9 olika primfaktorer
- kan skrivas på formen 12n + 1 eller 36n + 9
Olösta problem
Det finns flera olösta gåtor angående de perfekta talen:
- Man vet inte om det finns oändligt många perfekta tal.
- Hittills har alla perfekta tal man hittat slutat på 6 eller 28 (se uppställningen ovan). Men ingen har lyckats visa om alla perfekta tal gör det.
- Hittills har man inte lyckats hitta något udda perfekt tal. Men det är inte bevisat att det inte finns några sådana.
Se även
- Primtal
- Talteori
- Defekt tal
- Ymnigt tal
- kvasiperfekt tal
- Nästan-perfekt tal
- Superperfekt tal
- Sigmafunktionen
Externa länkar
Olika typer av matematiska tal
Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal



