Option
Från Rilpedia
Option är inom ekonomi en typ av derivat. En option ger innehavaren rätt, men inte skyldighet, att i en bestämd tidsperiod eller tidpunkt i framtiden köpa eller sälja den underliggande tillgången till ett på förhand bestämt pris.
Innehåll |
Option allmänt
Den underliggande tillgången är tillgången eller värdet som optionen ger rättighet att köpa eller sälja. Denna underliggande tillgång kan till exempel vara en aktie, valuta, råvara, obligation, ränta, option eller ett index. Ofta sker ingen fysisk leverans av den underliggande tillgången utan ägaren av optionen erhåller värdet för den tänkta transaktionen. Optioner är kapitalandelsbevis.
Köpoption och säljoption
En option som ger rätten att köpa en viss tillgång till ett förutbestämt pris kallas köpoption eller call. En option som ger rätten att sälja en tillgång till ett förutbestämt pris kallas säljoption eller put på anglifierad svenska.
Istället för att köpa en option kan man ställa ut en option. Att ställa ut en köpoption innebär att man är beredd att sälja en aktie för det förutbestämda priset om den andra parten utnyttjar sin rättighet. Man blir alltså motpart gentemot parten som istället köper samma form av option. Den som ställer ut en option sägs ha en kort position i optionen och den som köper en option sägs ha en lång position i optionen.
Den största förlusten som är möjlig när det gäller en lång position i en option är värdet som är investerat i optionen. Den största förlusten som är möjlig när det gäller en kort position i en option kan vara långt större och därför krävs ofta någon form av säkerhet för att få ställa ut optioner.
Olika typer av optioner
Om rättigheten som optionen innebär kan användas vid en specifik tidpunkt kallas optionen för europeisk. En option av amerikansk typ ger däremot ägaren rätt att lösa in optionen när denne vill fram till slutdagen. En amerikansk option innebär därmed större rättigheter än den europeiska vilket innebär att dess värde alltid måste vara större än eller lika med motsvarande europeiska. Talet om europeiska och amerikanska optioner ska inte sammanblandas med motsvarande kontinenter, eftersom optioner av både amerikansk och europeisk typ handlas över hela världen. De aktieoptioner som det handlas med i Sverige är av amerikansk typ.
Utöver dessa två vanligaste former av optioner finns också en rad andra så kallade exotiska optioner. För att särskilja den vanliga typen av optioner så kallas dessa ibland för ren vanilj-optioner (engelska: plain vanilla options).
En options värde på slutdagen
En köpoptions värde på slutdagen är lika med maximum av den underliggande tillgångens värde minus det förutbestämda priset och noll. Analogt med detta är en säljoptions värde på slutdagen lika med maximum av det förutbestämda priset minus den underliggande tillgångens värde och noll. Det hela kan förtydligas genom ett exempel: En köpoption med det förutbestämda lösenpriset 100 kronor köps och den underliggande tillgången är en aktie. På slutdagen handlas aktien för 110 kronor och därmed ger optionen rättighet att köpa en aktie som är värd 110 kronor för 100 kronor och en sådan rättighet är rimligen värd 10 kronor vilket också är optionens värde. Å andra sidan, om aktien handlas för 90 på inlösensdagen så har optionsinnehavaren fortfarande rätten att köpa aktien för 100. Denna rättighet är värdelös eftersom aktien handlas för ett lägre belopp på marknaden, så optionen löses inte in, och dess värde är noll. I och med att en option innebär en rättighet och ingen skyldighet så är en options värde aldrig negativ.
Optioner i Sverige
Standardiserade optioner har ofta en kortare löptid än ett år, till skillnad från warrant som ofta har längre löptid.
Optionsvärdering
Att bestämma en options värde vid en tidpunkt före slutdagen involverar däremot många fler komponenter.
För att kunna beräkna ett optionspris före slutdagen behöver man en stokastisk modell för den underliggande tillgången. Priset av en option skriven på den underliggande tillgången är sedan det värde som gör att en finansiell aktör inte kan skapa ett arbitrage genom att investera i optionen och i den underliggande tillgången. Eftersom värdet hos optionen på slutdagen vid olika pris på den underliggande tillgången är känt så kan ofta även optionens värde vid tidpunkter före slutdagen beräknas med hjälp av numeriska lösningsmetoder eller i vissa fall med analytiska uttryck.
Black–Scholes modell
I början av 70-talet publicerade Fisher Black, Myron Scholes och Robert Merton artiklar som skulle skapa ett genombrott när det gäller prissättningen av främst europeiska aktieoptioner genom att skapa vad som senare har kommit att kallas för Black–Scholes modell. Denna modell har stort inflytande över hur optioner prissätts och hedgas. Scholes och Merton erhöll 1997 Sveriges Riksbanks pris i ekonomisk vetenskap till Alfred Nobels minne för sina insatser. Black var redan avliden när priset utnämndes.
Black–Scholes modell är baserad på ett antal antaganden om den underliggande tillgångens stokastiska process och hur marknaden fungerar. Enligt Black–Scholes modell så påverkas en europeisk aktieoptions pris av fem faktorer.
- Den underliggande tillgångens pris
- Det förutbestämda priset
- Den underliggande tillgångens volatilitet
- Den riskfria räntan
- Den kvarvarande tiden till slutdagen.
De använde sig av ett antal antaganden bl.a.:
- Den underliggande tillgångens avkastning är normalfördelad och tillgångens pris är lognormalfördelad
- En arbitragefri marknad
Härledningen bygger på riskneutral värdering och användande av Itos lemma.
Formlerna för hur dessa faktorer hänger ihop är enligt Black–Scholes modell:
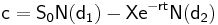
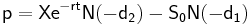
där
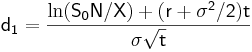
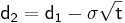
I denna formel så står S för nuvärdet av den underliggande tillgången. X står för det förutbestämda priset och r står för den riskfria räntan vidare så står t för tiden kvar till slutdagen och sigma står för volatiliteten. N(x) står för den kumulativa normalfördelningen, c står för värdet av en köpoption och p står för värdet av en säljoption.
Om formeln deriveras med hänsyn till de olika ingående komponenterna så fås de så kallade grekerna. Uppkallat efter de grekiska bokstäver som brukar användas som beteckningar. Dessa greker bildar känslighetsparametrar eller riskparametrar när det gäller optionens värdeförändring när de ingående parametrarnas värden förändras.
Modellen skapades för att beräkna värdet för europeiska aktieoptioner på aktier som inte ger utdelning. Men modellen har också visats sig mycket användbar på andra typer av optioner och den har också utvecklats i andra varianter för att kunna användas till andra former av optioner.
För mer okonventionella former av optioner, så kallade exotiska optioner, måste ibland användas andra metoder så som Monte Carlo-simulering eller trädmodeller när värdet ska beräknas.
Referenser
Skatteregler för optioner, Skatteverket



