Arbitrage
Från Rilpedia
Arbitrage (från lat. Arbitratus, fritt val) är en term som beskriver utnyttjandet av obalanser mellan två eller fler marknader, en kombination av matchande handelsmöjligheter utnyttjas för att utnyttja obalansen mellan marknaderna, som består av skillnader i marknadspriser. När termen används av akademiker så refererar den till en transaktion som inte involverar något negativt kassaflöde och i något läge skapar ett positivt kassaflöde, enkelt uttryckt en riskfri vinst. Termen används oftast vid handel av finansiella instrument så som obligationer, aktier, derivat och valutor.
Om marknadspriserna inte tillåter skapandet av arbitrage så sägs priserna uppfylla arbitrage equilibrium eller en arbitragefri marknad. En arbitragefri marknad är en förutsättning för en effektiv marknad.
Innehåll |
Förutsättningar för arbitrage
Arbitrage är möjligt när en av följande fem förutsättningar är uppfyllda:
- Samma tillgång handlas inte för samma pris på alla marknader.
- Två tillgångar med identiska kassaflöden handlas inte för samma pris.
- En tillgång med ett känt pris i framtiden handlas inte idag till sitt framtida pris diskonterat med den riskfria räntan. (eller så har tillgången en icke irrelevant kostnad för förvaring, som vissa råvaror men inte finansiella tillgångar har)
- Handel pågår vid samma tidpunkt på minst 2 olika marknadsplatser.
- Transaktionen avslutas vid samma tidpunkt både vad gäller köp och sälj av tillgången och transaktionen är därmed helt riskfri.
Exempel på arbitrage
- Antag att valutakurserna (med hänsyn tagen till växlingskostnader) i London är £5 = $10 = ¥1000 och att växlingskursen i Tokyo är ¥1000 = £6 = $10. Därmed är växling av $10 till £6 möjligt i Tokyo och i London är det möjligt att växla £6 till $12, och det hela skapar en vinst på $2, detta vore ett arbitrage. I realiteten är denna typ av "triangelarbitrage" så pass enkel att den nästan aldrig uppkommer. Men mer komplicerade valutaarbitrage så som avista-termin arbitrage är långt mycket mer vanliga.
Arbitrage inom finansiell matematik
I finansiell matematik definieras arbitrage genom att en (n + 1)-dimensionell aktiportfölj 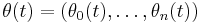 ,
, ![t \in [0, T]](/w/images/sv.rilpedia.org/math/e/6/6/e66a2b7fedcba80ccb192b87440f8d9c.png) , ska uppfylla de tre villkoren
, ska uppfylla de tre villkoren
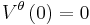 ,
,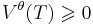 (nästan säkert med avseende på P),
(nästan säkert med avseende på P),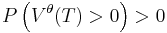 ,
,
för alla sluttider T > 0 där Vθ är värdet hos aktieportföljen och P är det relevanta sannolikhetsmåttet.
Referenser
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications. Springer, Berlin. ISBN 3-540-04758-1.



