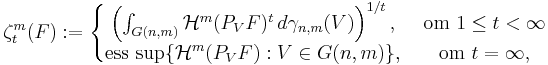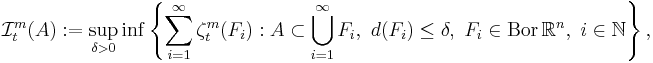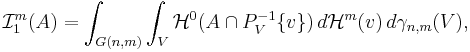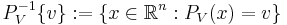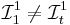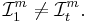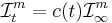Favardmått
Från Rilpedia
Ett Favardmått eller integralgeometriskt mått är inom matematik ett mått som är viktigt för rektifierbara mängder. Favardmåttet är namngett efter den franska matematikern Jean Favard som uppfann det.
Innehåll |
Formell definition
Favardmåttet är definierat med hjälp av Carathéodorys konstruktion. Man konstruerar det så att alla Borelmängder är testmängder och testmåttet är en speciell integral definierad med hjälp av Grassmannmåttet.
Mer precist, om  ,
, 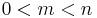 ,
, ![t \in [0,\infty]\,](/w/images/sv.rilpedia.org/math/6/0/3/6035be82f80bb854950d736b348c8dfc.png) och för
och för 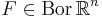
där
- mängden
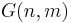 är Grassmannmångfalden,
är Grassmannmångfalden,
- måttet
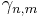 är Grassmannmåttet,
är Grassmannmåttet,
- integralen
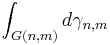 är måttintegralen med avseende på Grassmannmåttet
är måttintegralen med avseende på Grassmannmåttet 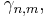
- funktionen
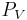 är ortogonal projektionen på delrummet
är ortogonal projektionen på delrummet 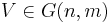 och
och
- operatorn
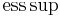 är väsentligt supremum med avseende på Grassmannmåttet
är väsentligt supremum med avseende på Grassmannmåttet 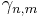 .
.
Då är yttre måttet ![\mathcal{I}^m_t : \mathcal{P}(X) \rightarrow [0,\infty],](/w/images/sv.rilpedia.org/math/8/1/5/8155d63180aff4ec5aed12ae3350f0d3.png) definierad som:
definierad som:
och detta är det m-dimensionella yttre Favardmåttet med konstanten 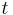 .
.
Konstanten t = 1
Där finns en lätt formel för Favardmåttet med konstanten 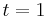 . Det går att visa att
. Det går att visa att
där
- måttet
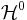 är det nolldimensionella Hausdorffmåttet, dvs räknemåttet, och
är det nolldimensionella Hausdorffmåttet, dvs räknemåttet, och
för 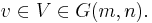
Rektiefierbara mängder
När konstanten t = 1 finns en intuitiv förklaring för namnet integralgeometriskt: låt 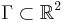 vara en rektifierbar kurva.
vara en rektifierbar kurva.
För en linje 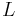 räkna (med räknemåttet) alla punkter i snittmängden
räkna (med räknemåttet) alla punkter i snittmängden  och integrera (dγ2,1) detta talet över alla linjer
och integrera (dγ2,1) detta talet över alla linjer 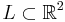 . Detta talet (Favardmåttet) är längden för kurvan
. Detta talet (Favardmåttet) är längden för kurvan 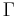 .
.
Generellt, för 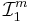 med
med 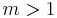 kan man sluta sig till samma utgång.
kan man sluta sig till samma utgång.
Egenskaper
Favardmåttets egenskaper är inte väl känt. Det går att visa att
när 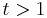 men man vet inte för vilka m > 1 det gäller att:
men man vet inte för vilka m > 1 det gäller att:
Dessutom man vet inte om det finns en konstant 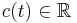 så att
så att
för alla 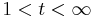 .
.
Referenser
- J. Favard, Une définition de la longueur et de l'aire, C. R. Acad. Sci. Paris vol. 194 p. 344, 1932.
- H. Federer, Geometric Measure Theory, Springer-Verlag, 1969.
- P. Mattila, Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability, Cambridge University Press, 1995.