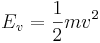Hastighet
Från Rilpedia
Hastighet är inom fysik en storhet för att beskriva rörelse. Storheten är definierad som förändring av läge per tidsenhet. Hastighet har dimension längd per tid och betecknas vanligen v, från latinets velocitas. I SI-systemet är dess enhet meter per sekund, som till exempel används för vindstyrka. En vardagligare enhet är kilometer per timme. Omräkningen är att 1 m/s = 3 600 m/h = 3,6 km/h.
Hastighet (momentanhastighet) är en vektor eftersom den har både storlek (fart) och riktning. Det är positionsvektorns tidsderivata, som vid varje tidpunkt är parallell med partikelns bana. Vektorstorheten skrivs 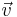 eller
eller 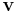 . Enligt Newtons rörelselagar är en kropps hastighet konstant om inga yttre krafter verkar på den. Olika inertialsystem är ekvivalenta, och någon absolut hastighet (eller absolut vila) kan inte definieras.
. Enligt Newtons rörelselagar är en kropps hastighet konstant om inga yttre krafter verkar på den. Olika inertialsystem är ekvivalenta, och någon absolut hastighet (eller absolut vila) kan inte definieras.
Medelhastighet avser vanligtvis tidsmedelvärdet av fart, där banan inte nödvändigtvis är rak. Medelfarten är lika med längden på avlagd sträcka delad med tidsintervallet. Vid flöden kan man tala om medelhastigheten vid en viss tidpunkt. Då avser man medelvärdet över en yta eller över vätskans volym, eller över alla partiklars hastighet som i drifthastighet.
Enligt relativitetsteorin är hastighet mer fundamental än längd och tid eftersom ljusets hastighet i vakuum där är lika för alla observatörer. Inom partikelfysik har ofta partiklarna hastigheter nära ljusets hastighet. I sådana fall är det mer relevant att tala om partiklarnas rörelseenergi.
Exempel på hastigheter
| Tiopotens | Värde (m/s) | Värde | Exempel |
|---|---|---|---|
| 10-9 | 0,3×10-9 till 3×10-9 | några cm/år | Typisk hastighet för kontinentaldrift. |
| 5×10-9 | cm/månad | Hårtillväxt, jämför skäggsekund. | |
| 10-3 | 0,0017 | decimeter/minut | Snigelfart.[1] |
| 100 | 1,5 | 5,4 km/h | Promenadhastighet. |
| 101 | 10,32 | 37,15 km/h | Medelhastighet av Usain Bolt på 100 m sprint. |
| 17 | 60 km/h | Medelhastighet av en galopphäst (Engelsk mil). | |
| 55,5 | 200 km/h | Maxhastighet för X 2000 | |
| 102 | 120 | 432 km/h | Signalhastighet på nerver med myelinskikt. |
| 130 | 468 km/h | Vindhastighet i en tornado. | |
| 161 | 580 km/h | JR-Maglev-tåget år 2003. | |
| 250 | 900 km/h | Typisk hastighet för ett trafikflygplan som Airbus A380. | |
| 331,5 | 1 193,4 km/h | Ljudhastighet i luft på havsnivå vid 0 °C. | |
| 464 | 4 000 mil/dygn | Rotationshastigheten vid jordens ekvator. | |
| 650 | 2 340 km/h | Flyghastighet av Concorde. | |
| 975 | 3 510 km/h | Mynningshastighet hos en M16 automatkarbin. | |
| 104 | 11 082 | 39 895 km/h | Människans fartrekord: hastigheten av Apollo 10. |
| 11 200 | 40 320 km/h | Flykthastighet från jorden. | |
| 29 800 | 107 280 km/h | Jordens banhastighet kring solen. | |
| 106 | 2 200 000 | 13,6 eV | Elektronens banhastighet i Bohrs atommodell. |
| 107 | 85 000 000 | 20 keV | Typisk hastighet av en elektron i ett katodstrålerör. |
| 108 | 299 792 458 | 30 cm/ns | Ljusets hastighet i vakuum. |
Härledningar

I mekanik är medelhastigheten v för ett objekt som flyttar sig en sträcka s under ett tidsintervall t enligt följande formel:
- v = s/t.
Vektorn för momentanhastighet v av ett objekt vars position vid tiden t ges av s(t) kan beräknas som derivatan
- v = ds/dt.
Acceleration är förändringen av ett objekts hastighet i en viss riktning, i tid. Medelaccelerationen a för ett objekt vars hastighet ändras från vi till vf under tidsintervallet t ges av:
- a = (vf - vi)/t.
Vektorn för momentanacceleration a av ett objekt vars position vid tiden t ges av x(t) är
- a = d2x/(dt)2
Sluthastigheten vf av ett objekt som startar med hastigheten vi och därefter accelerera med konstant acceleration a under tidsintervallet t är:
- vf = vi + at
Medelhastigheten för ett objekt i konstant acceleration är (vf + vi)/2. För att finna förflyttningen s av ett sådant accelererande objekt under tidsintervallet t, ger insättning av denna formel i den första formeln:
- s = t(vf + vi)/2
När endast objektets initialhastighet är känd, kan uttrycket
- s = vit + (a't2)/2
användas. Dessa grundläggande ekvationer för sluthastighet och förflyttning kan kombineras till en ekvation som är oberoende av tid, Toricellis formel, "tidlösa formeln" även kallad:
- vf2 = vi2 + 2as
Ovanstående ekvationer är giltiga för både klassisk mekanik och speciell relativitetsteori. Skillnaden mellan dessa är hur olika observatörer skulle beskriva samma situation. I klassisk mekanik är alla observatörer överens om värdet på 't' och transformeringsreglerna för position skapar en situation i vilken alla icke accelererande observatörer skulle beskriva ett objekts acceleration med samma värde. Ingetdera är sant inom relativitetsteorin.
Den kinetiska energin (rörelseenergi) för ett objekt i rörelse är proportionell mot både dess massa och kvadraten på farten:
Den kinetiska energin är en skalär kvantitet.
Noter
- ↑ Yee, Angie (1999). ”Speed of a Snail”. The Physics Factbook. http://hypertextbook.com/facts/AngieYee.shtml.