Banach-Steinhaus sats
Från Rilpedia
Inom den gren av matematiken som kallas funktionalanalys är Banach-Steinhaus sats eller satsen om likformig begränsning som den också kallas ett ofta använt resultat.
Banach-Steinhaus sats
- Låt X och Y vara två normerade vektorrum och
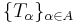 en familj av begränsade linjära operatorer
en familj av begränsade linjära operatorer 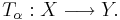 Denna familj besitter följande två egenskaper:
Denna familj besitter följande två egenskaper:
- Operatornormerna
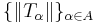 är begränsade om vektornormerna
är begränsade om vektornormerna 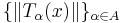 är begränsade, för varje punkt x i en icke-mager delmängd av rummet X.
är begränsade, för varje punkt x i en icke-mager delmängd av rummet X. - Operatornormerna
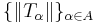 är begränsade om vektornormerna
är begränsade om vektornormerna 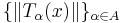 är begränsade, för varje punkt x i Banachrummet X.
är begränsade, för varje punkt x i Banachrummet X.
- Operatornormerna
Användning av Banach-Steinhaus sats
En omedelbar konsekvens av Banach-Steinhaus sats är den så kallade Principen om kondensation av singulariteter: Om X är ett Banachrum och Fn är en familj av obegränsade linjära operatorer från X till något annat linjärt rum Y så gäller att
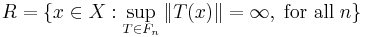 är tät i X.
är tät i X.
Ett annat viktigt resultat som kan visas med hjälp av Banach-Steinhaus sats är att de flesta kontinuerliga periodiska funktioner inte konvergerar punktvis till sin Fourierserieutveckling. Mer precist: för varje 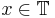 gäller att mängden av funktioner i
gäller att mängden av funktioner i 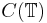 vars Fourierserie divergerar i x är tät i
vars Fourierserie divergerar i x är tät i 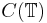 .
.
Det är också Banach-Steinhaus sats, tillsammans med det faktum att grafen till Wienerprocessen har ändlig kvadratisk variation, som tvingade fran begreppet stokastisk integral och därmed det nya området stokastisk analys.
Bevis av Banach-Steinhaus sats
Beviset bygger på Baires kategorisats och begreppet mager mängd.



