Baires kategorisats

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Baires kategorisats är ett fundamentalt begrepp inom funktionalanalys som bland annat ger upphov till de stora teoremen inom funktionalanalys: Banach-Schauders sats, satsen om den slutna grafen och Banach-Steinhaus sats. Satsen är uppkallad efter René-Louis Baire.

Baires kategoriteorem

Varje fullständigt metriskt rum X besitter följande två egenskaper:

  • Om 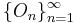\{O_n\}_{n=1}^\infty är en följd bestående av öppna och täta delmängder av X, så är deras snitt 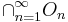\cap_{n=1}^\infty O_n\, också en tät delmängd av X.
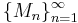  • Mängden X kan inte framställas som en uppräknelig union av ingenstans täta delmängder \{M_n\}_{n=1}^\infty : X \neq \bigcup_{n=1}^\infty M_n.
Hämtad från "https://sv.rilpedia.org/wiki/Baires_kategorisats"
Personliga verktyg