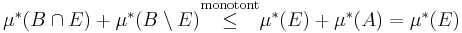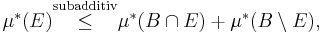Fullständigt mått
Från Rilpedia
Version från den 5 april 2009 kl. 08.43 av Petter Strandmark (Diskussion)
Ett fullständigt mått är ett begrepp inom matematisk måtteori. Ett mått är fullständigt om alla delmängder av nollmängder är mätbara. Dessa mängder kommer då nödvändigtvis ha måttet 0.
Innehåll |
Formell definition
Låt 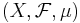 vara ett måttrum. Måttet µ är fullständigt om
vara ett måttrum. Måttet µ är fullständigt om
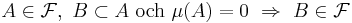 ,
,
dvs delmängder av A är mätbara mängder. Om måttet i måttrummet är fullständigt man kallas måttrummets fullständigt måttrummet.
Exempel
Alla mått som man har konstruerade med yttre mått vid Carathéodorys kriterion är fullständigt: om 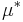 är ett yttre mått,
är ett yttre mått, 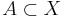 en µ*-mätbar mängd,
en µ*-mätbar mängd, 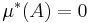 och
och 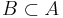 så är
så är
och
för alla 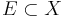 . Så att B är µ*-mätbar.
. Så att B är µ*-mätbar.
Därför är Lebesguemåttet och Hausdorffmåttet fullständiga mått.
Andra exempel är räknemåttet och Diracmåttet
Tillämpningar
- Man behöver fullständighet i Lp-rummets definitionen eftersom man vill integrera alla delmängder för en nollmängd.