Cayleys sats

Från Rilpedia

Texten från svenska Wikipedia

Cayleys sats är en matematisk sats inom gruppteori uppkallad efter Arthur Cayley som säger att varje grupp G är isomorf med någon permutationsgrupp. En följd av Cayleys sats är att allt som gäller för permutationsgrupper gäller för grupper i allmänhet.

Bevis

Beviset för Cayleys sats går ut på att det finns en undergrupp till den symmetriska gruppen på G, betecknad Sym(G), som är isomorf med G.

Tag ett a i G och definiera en avbildning 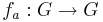som f_a(g) = ag för alla g i G. Bilda 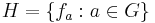, som är en delmängd till Sym(G).H är en grupp med funktionssammansättning som gruppoperation:

f_af_b(g) = f_a(f_b(g)) = f_a(bg) = abg = f_ab(g)

dvs, f_af_b = f_ab. Det neturala elementet 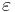i Sym(G) ligger i H eftersom 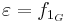. Inversen till f_a ges av 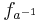. Detta ger att H är en grupp, specifikt en delgrupp till Sym(G).

H är i själva verket isomorf med G, ty 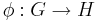definierad som φ(a) = f_a är en isomorfi:

φ är injektiv, ty om φ(a) = φ(b) är f_a = f_b som ger .

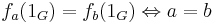Att φ är surjektiv följer ur definitionen.

Att φ är en grupphomomorfi, dvs att φ(a)φ(b) = φ(ab) följer ur f_af_b = f_ab.

De tre egenskaperna ovan ger att φ är en isomorfi. Alltså är gruppen G isomorf med permutationsgruppen H, vilket bevisar Cayleys sats.