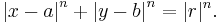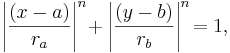Kvirkel

Från Rilpedia

Version från den 29 januari 2009 kl. 11.41 av Lelle1987 (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
En kvirkel

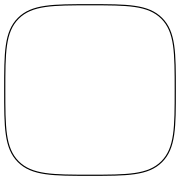
En kvirkel är en geometrisk figur med egenskaper från både en kvadrat och en cirkel. Det är ett specialfall av en superellips.

Innehåll

Ekvation

I ett Kartesiskt koordinatsystem, med kvirkeln centrerad kring punkten (a,b) samt axlar parallella mot koordinataxlarna, beskrivs den av ekvationen

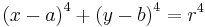
\left( x - a \right)^4 + \left( y - b \right)^4 = r^4

där r är den minsta radien i kvirkeln (jämför cirkelns ekvation).

Generalisering

Kvirkeln är ett specialfall (genom att sätta n = 4) i den geometriska figurklassen "supercirklar", som har ekvationen

\left| x - a \right|^n + \left| y - b \right|^n = |r|^n.\,

Supercirklar är sig en undergrupp till den mer generella "superellipsen", som har ekvationen

\left|\frac{\left( x - a \right)}{r_a}\right|^n\! + \left|\frac{\left( y - b \right)}{r_b}\right|^n\! = 1,\,

där ra och rb är de halva stor- och lillaxlarna. Superellipser studerades flitigt och myntades av den danske matematikern Piet Hein.

Liknande figurer

En kvirkel (svart) jämförd med en kvadrat med rundade hörn (röd) (se text)

En visuellt närliggande figur, en kvadrat med rundade hörn, kan skapas genom att distansera fyra jämnstora fjärdedelar från en cirkel, och sammankoppla deras ändar med räta linjer. Som man kan se i bilden bredvid, är en sådan figur snarlik, men ej identisk med kvirkeln. Även om en kvadrat med rundade hörn kan te sig konceptuellt lättare, så har kvirkeln en betydligt simplare ekvation och kan därför generaliseras enklare. Detta medför att kvirkeln och andra superellipser kan skalas upp och ner med lätthet, vilket är användbart när man exempelvis vill skapa nästlade kvirklar.

Användningsområden

Kvirklar är främst användbara inom optiken. Om man låter ljus passera genom en två-dimensionell kvadratformad bländare, kan "mittfläcken" i diffraktionsmönstret modelleras som en kvirkel, eller en supercirkel. Används istället en rektangelformad bländare, passar en superellips bra som approximation.[1]

Kvirklar har även använts till att formge tallrikar. En kvirkelformad tallrik har en större area (vilket ger mer plats för mat) än en cirkulär tallrik med samma radie, samtidigt som den tar upp lika mycket i plats i ett vanligt köksskåp.[2]

Microsoft's andra generation av den portabla mediaspelaren Zune, har utrustats med ett kvirkelformat scrollhjul.[3]

Se även

Källor

Denna artikel är helt eller delvis baserad på material från engelskspråkiga Wikipedia
  1. ↑ M. Fernández Guasti et al., Optik 116 s265–269, 2005. Finns online, Läst 20 november 2006
  2. ↑ Kitchen Contraptions, Squircle Plate, Läst 20 november 2006
  3. ↑ Zune Scene, Zune 2 October Launch, Läst 23 september 2007

Externa länkar

Hämtad från "https://sv.rilpedia.org/wiki/Kvirkel"
Personliga verktyg
På andra språk