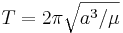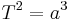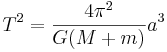Halv storaxel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Merge-arrow.svg
 En eller flera användare anser att denna text bör infogas i Ellips (matematik). (Diskussion)
Elps-slr.svg

Halva storaxeln används i geometrin för att beskriva storleken hos ellipser och hyperbler.

Innehåll

Ellipsen

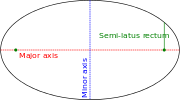
Storaxeln hos en ellips är dess längsta diameter, en linje som går genom mitten och bägge brännpunkterna, med ändpunkterna på de mest åtskilda delarna av figuren. Halva storaxeln är hälften av denna sträcka, från mitten genom en brännpunkt till ellipsens kant.

Halva storaxelns längd 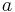a\! är knuten till halva lillaxeln 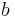b\,\! genom excentriciteten 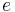e\,\! och semi-latus rectum 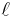\ell\,\! på följande sätt:

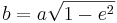
b = a \sqrt{1-e^2}\,\!
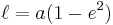\ell=a(1-e^2)\,\!.
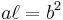a\ell=b^2\,\!.

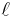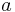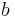En parabel är gränsfallet av en serie ellipser där en av brännpunkterna hålls konstant medan den andra tillåts avlägsna sig godtyckligt långt i en konstant riktning medan \ell\,\! hålls konstant. Alltså går a\,\! och b\,\! mot oändligtheten, 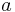a\,\! snabbare än b\,\!.

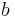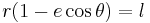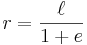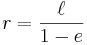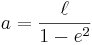Halva storaxel är medelvärdet av det största och minsta avståndet från en brännpunkt till punkterna på ellipsens omkrets. Betrakta nu ellipsens ekvation i polära koordinater, med en brännpunk i origo och den andra på den positiva x-axeln: r(1-e\cos\theta)=l\,\!. Medelvärdet av r={\ell\over{1+e}}\,\! och r={\ell\over{1-e}}\,\!, är a={\ell\over{1-e^2}}\,\!.

Hyperbel

Hyperbelns halva storaxel är hälften av avståndet mellan grenarna; om detta är a i x-axelns riktning blir ekvationen:

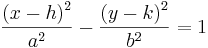
\frac{\left( x-h \right)^2}{a^2} - \frac{\left( y-k \right)^2}{b^2} = 1

Uttryckt i semi-latus rectum och excentriciten:

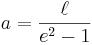
a={\ell\over e^2-1 }

Astronomi

Omloppstid

I astrodynamiken är omloppstiden 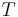T\, hos en liten kropp som kretsar runt en större centralkropp i en cirkulär eller elliptisk omloppsbana:

T = 2\pi\sqrt{a^3/\mu}

där:

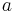a\, är omloppsbanans halva storaxel
μ är gravitationsparametern

Märk att alla ellipser med samma halva storaxel har samma omloppstid, oavsett excentriciteten.

I astronomin är halva storaxeln ett av de viktigaste banelementen i en omloppsbana. I solsystemet knyts halva storaxeln hos kroppar som kretsar run solen till omloppstiden av Keplers tredje lag,

T^2=a^3\,

där T omloppstiden mätt i år, och a är halva storaxeln mätt i astronomiska enheter. Detta uttryck visar sig vara ett specialfall av Isaac Newtons allmänna lösning av tvåkropparsproblemet:

T^2= \frac{4\pi^2}{G(M+m)}a^3\,

där G är gravitationskonstanten, M är centralkroppens massa och m är den kretsande kroppens massa. Oftast är centralmassan så mycket massivare än den kretsande kroppen att m kan försummas. Gör man det antagandet och använder man sig av typiska astronomienheter resulterar i Keplers enklare ekvation.

Medelavstånd

Det sägs ofta att halva längdaxeln är "medelavståndet" mellan huvudkroppen (vid en av ellipsens brännpunkter) och den kretsande kroppen. Detta är inte helt korrekt, eftersom det beror på hur medelvärdet beräknas:

  • medelvärdet över excentriska anomalin är faktiskt halva storaxeln.
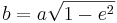  • medelvärdet över sanna anomalin (vinkeln mellan storaxeln, brännpunkten och kroppen) är konstigt nog halva lillaxeln b = a \sqrt{1-e^2}\,\!.
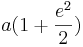  • medelvärdet över medelanomalin get slutligtvis tidsmedelsvärdet (vilket är vad "medelvärdet" oftast avses av lekmän) a (1 + \frac{e^2}{2})\,\!.


Referenser

Hämtad från "https://sv.rilpedia.org/wiki/Halv_storaxel"
Personliga verktyg