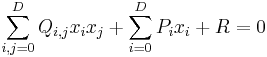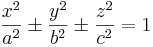Andragradsyta

Från Rilpedia

Version från den 2 mars 2008 kl. 16.07 av Yvwv (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

I matematik så är en andragradsyta, en D-dimensionell hyperyta definierad som lösningsmängden till ett kvadratiskt polynom. Med koordinater \{x_0, x_1, x_2, \ldots, x_D\}, så definieras den allmänna andragradsytan av ekvationen

\sum_{i,j=0}^D Q_{i,j} x_i x_j + \sum_{i=0}^D P_i x_i + R = 0

där Q är en D+1 dimensionell matris, P är en D+1 dimensionell vektor, och R en konstant. Värdena Q, P och R tas ofta som reella tal eller komplexa tal.

I normalform skrivs en tre-dimensionell (D=3) andragradsyta centrerad i origo (0,0,0) som:

\frac{x^2}{a^2} \pm \frac{y^2}{b^2} \pm \frac{z^2}{c^2}=1

Med translationer och rotationer kan varje andragradsyta transformeras till en av flera normalformer. I det tre-dimensionella euklidiska rummet finns 16 sådana normalformer. De mest intressanta är följande:

Yta Ekvation Plot
Ellipsoid x^2/a^2 + y^2/b^2 + z^2/c^2 = 1 \, Quadric Ellipsoid.jpg
Rotationsellipsoid eller sfäroid (specialfall av ellipsoid)   x^2/a^2 + y^2/a^2 + z^2/b^2 = 1 \,
Sfär (specialfall av rotationsellipsoid) 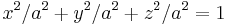x^2/a^2 + y^2/a^2 + z^2/a^2 = 1 \,
Elliptisk paraboloid 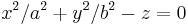x^2/a^2 + y^2/b^2 - z = 0 \, Quadric Elliptic Paraboloid.jpg
Cirkulär paraboloid (specialfall av elliptisk paraboloid) 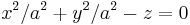x^2/a^2 + y^2/a^2 - z = 0 \,
Hyperbolisk paraboloid 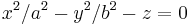x^2/a^2 - y^2/b^2 - z = 0 \, Quadric Hyperbolic Paraboloid.jpg
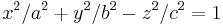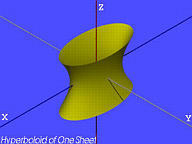Enmantlad hyperboloid x^2/a^2 + y^2/b^2 - z^2/c^2 = 1 \, Quadric Hyperboloid 1.jpg
Tvåmantlad hyperboloid x^2/a^2 - y^2/b^2 - z^2/c^2 = 1 \, Quadric Hyperboloid 2.jpg
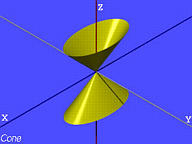kon x^2/a^2 + y^2/b^2 - z^2/c^2 = 0 \, Quadric Cone.jpg
Elliptisk cylinder 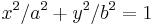x^2/a^2 + y^2/b^2 = 1 \, Quadric Elliptic Cylinder.jpg
Cirkulär cylinder (specialfall av elliptisk cylinder) 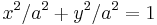x^2/a^2 + y^2/a^2 = 1 \,
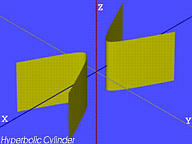
Hyperbolisk cylinder 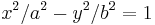x^2/a^2 - y^2/b^2 = 1 \, Quadric Hyperbolic Cylinder.jpg
Parabolisk cylinder x^2 + 2y = 0 \, Quadric Parabolic Cylinder.jpg

Se även

Länkar

  • [1], Quadrics in Geometry Formulas and Facts av Silvio Levy, utdrag från 30:e upplagan av "CRC Standard Mathematical Tables and Formulas (CRC Press)".
Hämtad från "https://sv.rilpedia.org/wiki/Andragradsyta"
Personliga verktyg
På andra språk