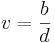Från Rilpedia

Randvinkelsatsen (periferivinkelsatsen) säger att medelpunktsvinkeln till en cirkelbåge är dubbelt så stor som en randvinkel som står på samma båge.

Medelpunktsvinkeln till en båge är den vinkel som har sin spets i cirkelns medelpunkt och vinkelbenen genom ändpunkterna på den del av cirkelns omkrets som är den betraktade cirkelbågen.

En randvinkel (eller periferivinkel) till en cirkelbåge har vinkelben genom bågens ändpunkter och sin spets på den del av cirkelns rand (=periferi=omkrets) som inte utgörs av den studerade bågen.

En generell formulering säger att om två linjer skär varandra i det inre, eller på randen, av en cirkel med diametern d, så skär de i en vinkel

där b är den sammanlagda längden av de bågar som linjerna skär av i det område där vinkeln mäts och det motstående. Ur denna formulering följer randvinkelsatsen som ett specialfall, eftersom linjer som skär på randen skär av en båge medan linjer som skär i medelpunkten skär av två bågar. Om de inblandade bågarna antas vara lika långa följer att vinkeln blir hälften så stor på randen som i medelpunkten.

Ett viktigt specialfall av randvinkelsatsen är när medelpunktsvinkeln är en rak vinkel och därmed randvinkeln en rät vinkel. Enligt sägnen offrade Thales 100 oxar till gudarna när han gjorde denna upptäckt. Detta är ett korollarium, som också kan uttryckas som att en rätvinklig triangels omskrivna cirkels medelpunkt ligger på hypotenusan.

Ett vanligt bevis för randvinkelsatsen är en tillämpning av Euklides första kongruensfall (s.k. "pusselgeometri") och yttervinkelsatsen, i vilken parallellaxiomet spelar en avgörande roll. Därmed gäller inte randvinkelsatsen i icke-euklidisk geometri.

En viktig konsekvens av randvinkelsatsen är kordasatsen som är en sats ur likformighetsgeometrin, i likhet med till exempel transversalsatsen och topptriangelsatsen.