Från Rilpedia

Den här artikeln anses undermålig och kan behöva skrivas om helt för att leva upp till Wikipedias artikelstandard. Diskutera frågan på diskussionssidan och förbättra gärna artikeln. Var uppmärksam på artikelns innehåll.

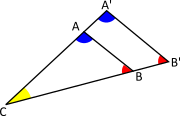
Transversalsatsen är en grundläggande sats för trianglar. Den säger att givet en triangel ABC och en med en av triangelns sidor, säg AB, parallellt dragen transversal A'B', kommer CB:BB' = CA:AA'. Den säger, i stort, att om vinklarna i två trianglar är desamma kommer trianglarna också att vara likformiga. Det känns visuellt helt intuitivt.

Man kan notera att dels beror satsen på parallellaxiomet, dels bevisas satsen i Euklides Elementa genom att nyttja en uppsättning axiom för area. Likformighet införs alltså logiskt via axiomen för area, men även omvänd väg är möjlig. Area och likformighet är därför mycket nära sammankopplade.

Topptriangelsatsen kan relativt enkelt härledas ur transversalsatsen. Det första (SAS) och det andra likformighetsfallet (SSS) beror då direkt på topptriangelsatsen. Och tredje likformighetsfallet (AAA) är i princip transversalsatsen själv.

Det är alltså ingen överdrift att säga att denna sats ligger till grund för hela likformighetsgeometrin.