Likformighet

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Denna artikel behandlar det geometriska begreppet likformighet. Se även likformig kontinuitet

Likformighet är inom geometri när två objekt är identiska sånär som på skalan.

Trianglar

Om en triangel 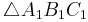\triangle A_1B_1C_1\ är likformig med en triangel 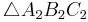\triangle A_2B_2C_2\ gäller

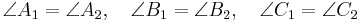
  • Motsvarande vinklar är lika \angle A_1 = \angle A_2, \quad \angle B_1 = \angle B_2, \quad \angle C_1 = \angle C_2 \
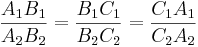
  • Skalan \frac{A_1B_1}{A_2B_2} = \frac{B_1C_1}{B_2C_2} = \frac{C_1A_1}{C_2A_2} \
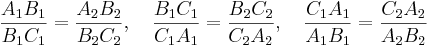
  • Förhållandet mellan motsvarande sidor är lika \frac{A_1B_1}{B_1C_1} = \frac{A_2B_2}{B_2C_2}, \quad \frac{B_1C_1}{C_1A_1} = \frac{B_2C_2}{C_2A_2}, \quad \frac{C_1A_1}{A_1B_1} = \frac{C_2A_2}{A_2B_2}

Två trianglar är likformiga om något av följande är uppfyllt:

  • VVV: Motsvarande vinklar är lika. Det räcker att två är lika, ty då är den sista vinkeln också samma.
  • SSS: Förhållandet mellan de tre sidparen är lika
  • SVS: Förhållandet mellan två sidpar är lika och mellanliggande vinkel är samma.


E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Likformighet"
Personliga verktyg