Rörelsemängdsmoment
Från Rilpedia

Inom fysiken är rörelsemängdsmomentet (impulsmomentet) för ett objekt som roterar kring någon referenspunkt, ett mått på i vilken utsträckning objektet kommer att fortsätta att rotera kring denna punkt när det påverkas av ett yttre vridmoment.
Om ett objekt roterar kring en axel är objektets rörelsemängdsmoment med avseende på en punkt på axeln relaterad till objektets massa, dess hastighet och dess tyngdpunkts avstånd till axeln.
Rörelsemängdsmoment är viktigt inom fysiken därför att det är en konserverad storhet: ett systems rörelsemängdsmoment förblir konstant till dess det påverkas av ett externt vridmoment. Vridmomentet är den hastighet med vilket rörelsemängdsmoment transfereras till eller från systemet. När en fast kropp roterar mäts dess motstånd mot en förändring av sin rotation av dess tröghetsmoment.
Rörelsemängdsmoment är ett viktigt begrepp inom både fysik och ingenjörsvetenskap och har otaliga tillämpningar. Ett exempel är beräkningar av den rörelseenergi och rörelsemängd som finns upplagrad i roterande kroppar, till exempel svänghjul.
Innehåll |
Rörelsemängdsmoment inom klassisk mekanik

Definition
Rörelsemängdsmomentet L för en partikel kring något centrum är definierad som kryssprodukten
där r är partikelns positionsvektor relativt centrum och p är partikelns rörelsemängd.
Den härledda SI enheten för rörelsemängdsmoment är newton·meter·sekunder; N·m·s (kgm2s-1).
På grund av kryssprodukten är L en pseudovektor vinkelrät mot både den radiella vektorn r och rörelsemängdvektorn p.
Om ett system består av flera partiklar är det totala rörelsemängdsmomentet med avseende på en axel summan av rörelsemängdsmomenten för de ingående partiklarna. Rörelsemängdsmomentet kan också beräknas genom att multiplicera kvadraten på avståndet till axeln med partikels massa och med dess vinkelhastighet. För en stel kropp gäller att 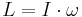 , där I är kroppens tröghetsmoment kring en viss axel och ω är vinkelhastigheten.
, där I är kroppens tröghetsmoment kring en viss axel och ω är vinkelhastigheten.
Rörelsemängdsmoment inom kvantmekaniken
Inom kvantmekaniken är rörelsemängdsmomentet kvantiserad, det vill säga det kan inte variera kontinuerligt, utan endast mellan specifika tillåtna värden. Rörelsemängdsmomentet för en subatomisk partikel, beroende på dess rörelse genom rummet, är alltid en heltalsmultipel av 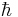 , definierad som Planks konstant dividerad med 2π.
, definierad som Planks konstant dividerad med 2π.
Experiment har visat att de flesta subatomiska partiklarna har ett permanent, inbyggt rörelsemängdsmoment, vilket inte har att göra med deras rörelse genom rummet. Detta spinn, rörelsemängdsmoment, förekommer i enheter av 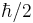 . Till exempel, en elektron i vila har ett rörelsemängdsmoment av
. Till exempel, en elektron i vila har ett rörelsemängdsmoment av 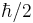 .
.
Grundläggande definitioner
Den klassiska definitionen av rörelsemängdsmoment som
beror av sex tal:
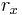 ,
, 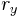 ,
, 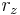 ,
, 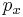 ,
, 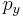 , och
, och 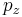 .
.
Osäkerhetsrelationen innebär att det inte är möjligt att mäta alla dessa värden samtidigt med godtycklig noggrannhet. Detta innebär att det finns gränser för med vilken noggrannhet rörelsemängdsmomentet kan vara känt eller kan mätas. Det visar sig att det bästa som går att åstadkomma är att samtidigt mäta rörelsemängdsmomentsvektorns amplitud och en av dess komponenter.
Inom kvantmekaniken definieras inte rörelsemängdsmomentet som en kvantitet utan som en operator för vågfunktionen
där 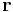 och
och 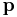 är position- respektive rörelsemängdsmomentoperatorn. Speciellt, för en enskild partikel utan elektrisk laddning och spinn, kan rörelsemängdsmomentet skrivas som
är position- respektive rörelsemängdsmomentoperatorn. Speciellt, för en enskild partikel utan elektrisk laddning och spinn, kan rörelsemängdsmomentet skrivas som
där 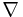 är gradientoperatorn. Denna orbitala rörelsemängdsmomentoperator är den vanligast förekommande formen av rörelsemängdsmomentoperator. Den satisfierar följande kommutativa relation
är gradientoperatorn. Denna orbitala rörelsemängdsmomentoperator är den vanligast förekommande formen av rörelsemängdsmomentoperator. Den satisfierar följande kommutativa relation
![[L_i, L_j ] = i \hbar \epsilon_{ijk} L_k](/w/images/sv.rilpedia.org/math/4/0/f/40fefc17eb2573272a68c336d1f92cc3.png) ,
,
där εijk är den (antisymmetriska) Levi-Civita symbolen. Av detta följer
Då,
följer till exempel,




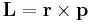
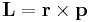
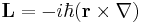
![\left[L_i, L^2 \right] = 0](/w/images/sv.rilpedia.org/math/a/9/9/a993bc5be027b1e1fdc595125ad4d91e.png)
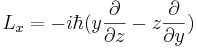
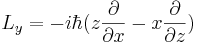
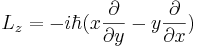
![\begin{align}
\left[L_x,L_y\right] & = -\hbar^2 \left( (y {\partial \over \partial z} - z {\partial\over \partial y})(z {\partial\over \partial x} - x {\partial\over \partial z}) - (z {\partial\over \partial x} - x {\partial\over \partial z})(y {\partial \over \partial z} - z {\partial\over \partial y})\right) \\
& = -\hbar^2 \left( y {\partial\over \partial x} - x {\partial\over \partial y}\right) = i \hbar L_z. \\
\end{align}](/w/images/sv.rilpedia.org/math/5/f/8/5f8334a26a0f562abddef2868f119a81.png)