Oegentlig rotation
Från Rilpedia
En oegentlig rotation (även rotoinversion) är en vanlig rotationsavbildning av ett reellt tredimensionellt rum R3 som håller origo fixt, följt av en spegling i origo (x går till -x). En oegentlig rotation på ett objekt är alltså en rotation på objektets spegelbild. Oegentliga rotationer beskrivs med 3×3 ortogonalmatriser med determinanten -1. Operationen betecknas ofta som 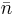 för en oegentlig rotation 360°/n. Notera att spegling i planet även kan skrivas
för en oegentlig rotation 360°/n. Notera att spegling i planet även kan skrivas 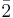 .
.
(Dess motsvarighet, egentlig rotation, är en vanlig rotation som har determinanten 1.)
Produkten av två oegentliga rotationer är en egentlig rotation. Produkten mellan en oegentlig och egentlig rotation är en oegentlig rotation.
När man studerar symmetrin på ett fysikaliskt system under en oegentlig rotation är det viktigt att göra skillnad mellan vektorer och pseudovektorer (likväl mellan skalärer och pseudoskalärer; eller mer generellt tensorer och pseudotensorer. Detta beror på att transformationen skiljer sig mellan egentliga och oegentliga rotationer (pseudotensorer är invarianta under inversion).



