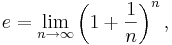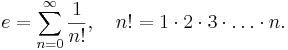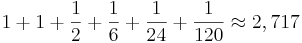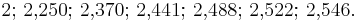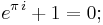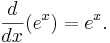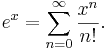e (tal)

Från Rilpedia

(Omdirigerad från Nepers tal)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Sökning på "Eulers tal" leder hit. Inte att förväxlas med Eulertal och Eulers konstant.

Talet e är den matematiska konstant som utgör basen för den naturliga logaritmen, ln. Det fick sin nuvarande beteckning av Leonhard Euler och kallas efter honom ibland Eulers tal, och är ungefär lika med 2,718.

Talet kan definieras som gränsvärdet

e = \lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n,

eller serien

e= \sum_{n = 0}^{\infty}\frac{1}{n!}, \quad n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n.


Talet e är ett irrationellt tal. Adderar man några av de första termerna i serien ovan, säg

1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} \approx 2,717

får man en hygglig approximation till e (två korrekta decimaler) vars decimalutveckling börjar 2,718 281 828 459 045... och fortsätter i all oändlighet utan någon synbar systematik i decimalföljden. De sju första elementen i talföljden 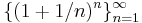\{(1+1/n)^n\}_{n=1}^\infty är följande:

2, 9/4, 64/27, 625/256, 7776/3125, 117649/46656, 2097152/823543.

I decimalform, avrundat till tre decimaler:

2; \, 2{,}250; \, 2{,}370; \, 2{,}441; \, 2{,}488; \, 2{,}522; \, 2{,}546.

Talföjden konvergerar tydligen ganska långsamt mot talet e.

Talet förekommer lite varstans i matematiken; bland annat råder följande samband mellan nio av matematikens mest använda objekt:

e^{\pi \, i} + 1 = 0;

Objekten som avses är: Operationerna addition, multiplikation, exponentiering och likhet samt talen e, π, i, 1 och 0. (Symbolen i betecknar den så kallade imaginära enheten och är det objekt med vilken de komplexa talen är uppbyggda.)

År 1873 bevisade Charles Hermite att talet e även är ett transcendent tal. Det var därmed det första exemplet på ett "naturligt förekommande" transcendent tal.

Den kanske viktigaste egenskapen hos talet e är att exponentialfunktionen, som den ger upphov till, är en fixpunkt till deriveringsoperatorn; med andra ord är exponentialfunktionen opåverkad om man deriverar den:

{d \over dx}(e^x) = e^x.

Med utgångspunkt från definitionen av talet e som en serie, kan exponentialfunktionen också definieras som en serie:

e^x = \sum_{n=0}^\infty \frac{x^n}{n!}.

Serien ovan kan även användas för att ge en definition av exponentialfunktionen i komplex mening, och kan användas som motivation till Eulers formel.

Typografisk aspekt

Enligt den svenska standarden SS 03 61 07 (Grafisk teknik – Sättningsregler – Matematik och kemi) ska e som beteckning för den naturliga logaritmen inte skrivas i kursiv stil, då den är en matematisk konstant och inte en variabel. Detta följs dock inte i någon utsträckning alls, då konstanter också skrivs i kursiv stil.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/E_(tal)"
Personliga verktyg