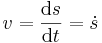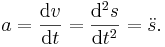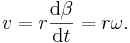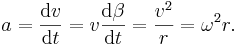Rörelse (fysik)
Från Rilpedia
Rörelse är i fysik lägesändring av en kropp. Beskrivningen av läge som funktion av tid är kinematik, en gren av klassisk mekanik. Grundbegrepp är position, hastighet och acceleration, som i två och tre dimensioner beskrivs med vektorer.
Innehåll |
Historia
I enlighet med erfarenhet och observation lärde Aristoteles att de jordiska tingens naturliga tillstånd var vila. Rörelse kom till ett slut, eftersom kroppar strävade efter vila. Endast himlakroppars rörelse var konstant, eftersom deras naturliga tillstånd var cirkulär rörelse.
Mekaniken utvecklades under medeltiden, och fann sitt moderna sätt att betrakta rörelse hos Galilei och Newton. Här är det inte något speciellt med vila, eftersom rörelse och vila är relativa begrepp. En kropp i rörelse utan yttre påverkan fortsätter sin rörelse, med samma fart och i samma riktning.
Rätlinjig rörelse
Rörelse längs en rak linje kan ritas som en matematisk funktion av avstånd eller position som funktion av tid. Man kan också rita kroppens hastighet eller dess acceleration som funktion av tid. Dessa funktioner har en matematisk relation till varandra: hastighet är positionens derivata med avseende på tid. Acceleration är hastighetens tidsderivata, eller positionens andraderivata:
Figuren till höger visar ett exempel. Den gröna linjen anger läge som funktion av tid. Först är kroppen i vila, sedan börjar den röra på sig. Den blå kurvan visar att hastigheten är konstant under en tid, till kroppen stannar en stund, börjar röra sig åt motsatt håll och stannar nära utgångsläget. Acceleration är skilt från noll endast när hastigheten ändrar sig. Enligt Newtons rörelselagar är det endast då att det verkar en kraft på kroppen.
Några specialfall av rätlinjig rörelse är likformig rörelse (när hastigheten är konstant) och likformigt föränderlig rörelse (när accelerationen är konstant). Ett annat specialfall är harmonisk rörelse, när kroppens läge oscillerar fram och tillbaka enligt en sinusfunktion.
Kroklinjiga rörelser
Kroklinjiga rörelser kräver beskrivning med två eller tre rymdkoordinater. Såväl läge som hastighet och acceleration är vektorer, med båda storlek och riktning. Hastighet är ändring i position och dess riktning är parallell med kroppens bana. Så är inte nödvändigtvis fallet med acceleration. När farten (hastighetens storlek) ändrar riktning, är accelerationen inte parallell med rörelseriktningen. Även här finns specialfall. Enklast är uniform cirkulär rörelse och kastparabelen.
Uniform cirkulär rörelse
Vid uniform cirkulär rörelse färdas en partikel med konstant fart över en cirkelbana. Rörelsen kan beskrivas med banans radie R och partikelns vinkelhastighet ω, som är tidsderivatan av vinkelläget β. Vinkelhastigheten har SI-enheten radian per sekund. Partikelns fart är
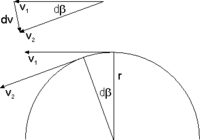
Figuren till höger visar att den infinitesimala ändringen i hastigheten dv är riktad mot cirkelns centrum och att dess storlek är proportionell mot hastigheten och mot dβ. Accelerationen ges av
Externa länkar
 Wikimedia Commons har media som rör Rörelse (fysik)
Wikimedia Commons har media som rör Rörelse (fysik)