Från Rilpedia

Konvergens är inom matematik en egenskap hos vissa talföljder, det vill säga sekvenser av tal x_i. Dessa är konvergenta om de närmar sig ett fixt tal x. Med att en summa är konvergent menas att följden av dess partialsummor är konvergent.

Formellt är en följd 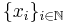i ett metriskt rum X konvergent om det finns ett element x i rummet X sådant att

För varje ε > 0 så finns 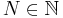så att om i > N så gäller

d(x_i,x) < ε.

I ett allmänt topologiskt rum X sägs följden 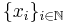konvergera mot x, om det för varje omgivning U till x gäller att 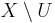endast innehåller ändligt många element från följden ovan.

Motsatsen är att följden är divergent.

I ett fullständigt metriskt rum är alla Cauchy-följder konvergenta. Stolz-Cesàros sats kan användas för att avgöra om en serie är konvergent.

Exempel

1. I R är talföljden 1, 1/2, 1/4, 1/8, ... konvergent, och den konvergerar mot 0. Talföljden 1, 1+1/2, 1+1/2+1/4, ... konvergerar även den, i detta fallet mot 2.
2. I rummet av alla reella tal större än (eller lika med) 0, konvergerar följden 1, 1/2, 1/3, 1/4, ... mot 0. Däremot är följden 1, 1+1/2, 1+1/2+1/3, ..., den harmoniska serien, divergent och växer mot oändligheten.

Funktionsföljder

Man kan också betrakta konvergens av en följd av funktioner f_n definierade på något Intervall, I, av de reella talen. Man säger att f_n konvergerar punktvis till f om 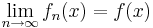för alla x i I.