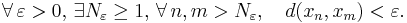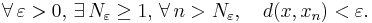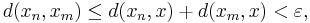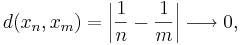Cauchy-följd

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
En Cauchyföljd, de blåa punkterna kommer närmare och närmare.
En följd som inte är en Cauchyföljd.

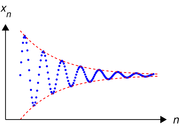
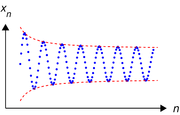
En Cauchy-följd är en talföljd, uppkallad efter den franske matematikern Augustin Louis Cauchy, där skillnaden mellan två på varandra följande tal hela tiden minskar och kan göras godtyckligt liten genom att gå ett ändligt antal steg i talföljden.

Begreppet är svagare än den vanliga konvergensen, det vill säga varje konvergent talföljd är också Cauchy-konvergent, medan det finns Cauchy-konvergenta talföljder som inte är konvergenta.

Ett rum i vilket alla Cauchy-följder är konvergenta kallas komplett eller fullständigt.

Definition

I ett metriskt rum, 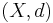(X,d)\,, är en sekvens av element 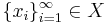\{x_i\}_{i=1}^\infty \in X en Cauchy-följd — även kallad Cauchy-sekvens — om avståndet mellan element, 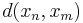d(x_n,x_m)\,, går mot noll då index n och m går mot oändligheten oberoende av varandra :

\forall \, \varepsilon > 0, \, \exists N_\varepsilon \geq 1, \, \forall \, n,m > N_\varepsilon, \quad d(x_n,x_m) < \varepsilon.

Nedan följer ett bevis av att en konvergent följd i ett metriskt rum också är en Cauchy-följd.

En följd 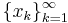\{x_k\}_{k=1}^\infty av element i ett metriskt rum (X,d) konvergerar mot ett element 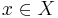x \in X om avståndet mellan x och xn går mot noll då index n går mot oändligheten :
\forall \, \varepsilon > 0, \, \exists \, N_\varepsilon \geq 1, \, \forall \, n>N_\varepsilon, \quad d(x,x_n) < \varepsilon.
Om vi väljer två index 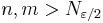n,m > N_{\varepsilon/2} oberoende av varandra, så ger triangelolikheten att avståndet mellan elementen xn och xm kan begränsas uppåt:
d(x_n,x_m) \leq d(x_n,x) + d(x_m,x) < \varepsilon,
vilket visar att 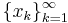\{x_k\}_{k=1}^\infty är en Cauchy-följd.

Exempel

Följande exempel visar att huruvida en Cauchy-följd konvergerar eller ej, har att göra med det metriska rummet (X,d) och inte med själva Cauchy-följden.

Låt det metriska rummet vara det öppna intervallet (0,1) tillsammans med metriken
d(x,y) = \vert x - y \vert (absolutbeloppet av talet 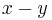x - y \,).
Sekvensen 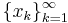\{x_k\}_{k=1}^\infty definierad som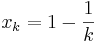 x_k = 1 - \frac{1}{k}
är en Cauchy-följd, eftersom avståndet mellan två godtyckliga element
d(x_n,x_m) = \left\vert \frac{1}{n} - \frac{1}{m}\right\vert \longrightarrow 0,
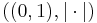då index n,m \longrightarrow \infty oberoende av varandra. Följden konvergerar mot talet 1, men detta tal är inte ett element i det metriska rummet ((0,1),\vert \cdot \vert). Därför konvergerar Cauchy-följden inte i det givna metriska rummet.
Hämtad från "https://sv.rilpedia.org/wiki/Cauchy-f%C3%B6ljd"
Personliga verktyg