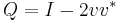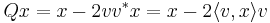Householdertransformation
Från Rilpedia
En Householdertransformation är inom matematiken, specifikt linjär algebra, en avbildning som i ett tredimensionellt ändligdimensionellt vektorrum med skalärprodukt reflekterar en vektor i ett plan (som innehåller origo, ett underrum). Detta kan generaliseras till alla ändligtdimensionella vektorrum som reflektion av en vektor i ett hyperplan som innehåller origo.
Transformationen kan även generaliseras till allmänna inre produktrum och kallas då Householderoperator. Transformen introducerades av Alston Scott Householder 1958.
Konstruktion och egenskaper
Ett hyperplan π kan definieras med dess normerade normalvektor, v (vektorn av längd 1 som är ortogonal till hyperplanet). Då ges Householdermatrisen Q av:
Där I är enhetsmatrisen och v * är det hermiteska konjuatet av v. Q reflekterar en punkt x i π, ty:
Där 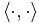 är skalärprodukten. Detta på grund av att
är skalärprodukten. Detta på grund av att 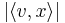 ger avståndet mellan x och π.
ger avståndet mellan x och π.
Q har ett antal bra egenskaper:
- Q är hermitesk: Q = Q * .
- Q är unitär: Q * = Q − 1.
- Av detta följer att Q är sin egen invers: Q2 = I.
Vilket stämmer bra då reflektionen av x:s reflektion måste vara x.
Användning
Householdertransformationer kan användas för att QR-faktorisera en matris.