Osäkerhetsprincipen
Från Rilpedia
| Kvantmekanik |
|---|
|
Teori:
Persongalleri |
| Den här artikeln saknar källhänvisningar. Förbättra gärna artikeln genom att lägga till pålitliga källor (helst fotnoter). Material som inte kan verifieras kan ifrågasättas eller tas bort. (juni 2009) |
-
- Denna artikel handlar om mätosäkerhet inom kvantfysiken. För andra mätningar se Mätosäkerhet.
Inom kvantfysiken anger Heisenbergs osäkerhetsprincip att man inte samtidigt kan känna både position och rörelsemängd med godtycklig precision hos ett objekt utan det finns en bestämbar undre gräns för osäkerheten. Den är en av hörnstenarna inom kvantmekaniken och upptäcktes av Werner Heisenberg 1927.
Osäkerhetsprincipen förklaras ibland genom påståendet att mätning av en partikels position nödvändigtvis orsakar en påverkan (störning) av partikelns rörelsemängd. Heisenberg gav själv den förklaringen ursprungligen. Det beror inte på störningen emellertid, eftersom principen även gäller om positionen mäts på en kopia av systemet, och rörelsemängden mäts i det andra identiska. Det är mer precist att säga att partikeln är en vågfunktion, inte ett punktliknande objekt, och inte kan ha både väldefinierad position och rörelsemängd. Av detta skäl rekommenderas numera termen "Heisenbergs obestämbarhetsrelation" (en: indeterminacy relations); någon osäkerhet råder inte.
Betrakta följande analogi: antag att man har en tidsvariant signal, som en ljudvåg, och man vill veta den exakta frekvensen för signalen i ett bestämt ögonblick. Detta är omöjligt. För att bestämma frekvensen exakt måste man sampla signalen under en viss tid och därmed förloras en viss grad av precision beträffande positionen. Med andra ord, ett ljud kan inte ha både exakt tid, som i en kort puls, och en exakt frekvens, som i en kontinuerlig ton. Fas och frekvens för en våg i tidsplanet är analoga med position och rörelsemängd för en våg i rummet.
Osäkerhetsprincipen är relaterad till ett annat kvantmekaniskt fenomen känt som vågfunktionskollaps i vilket själva observationen av en partikel tycks ändra ekvationerna som beskriver partikeln. Osäkerhetsprincipen anger att en partikel saknar fixt värde för rörelsemängd och position, men när man observerar en partikel tycks den inta ett fixt och distinkt värde för den kvantitet som mäts.
Innehåll |
Definition
Om flera identiska kopior av ett system i ett givet tillstånd prepareras, kommer mätningar av position och rörelsemängd att variera enligt kända sannolikhetsfördelningar; detta är det fundamentala postulatet om kvantmekanik. Vi skulle kunna mäta standardavvikelsen Δx av positionsmätningarna och standardavvikelsen Δp av rörelsemängdsmätningarna. Därefter skulle vi finna att
där h-streck är Plancks konstant delad med 2π. (I vissa behandlingar av ämnet väljs "osäkerheten" av en variabel så att den motsvarar det smalaste omfånget som innehåller 50% av värdena, som, i fallet normalfördelade variabler, leder till en snävare gräns än h/2π för produkten av osäkerheter.) Notera att denna olikhet medger flera möjligheter: tillståndet och mätförfarandet skulle kunna vara sådant att x kan mätas med hög precision, men då blir p endast approximativt känt, eller omvänt, p skulle kunna vara skarpt definierad medan x inte kan bestämmas precis. I andra tillstånd kan både x och p mätas med rimlig (men ej godtycklig) precision. I vardagslivet observerar vi inte dessa osäkerheter därför att värdet av h är extremt litet, och den relativa osäkerheten blir därmed extremt liten.
Samma relation gäller mellan energi och tid, till exempel mellan livstid av ett exciterat tillstånd och spektrallinjens bredd ΔE:
Eftersom för ljus gäller att ΔE = h Δν, kan man se detta som Fourieranalysens samband mellan osäkerheten i frekvens Δν och signalens tidslängd.
Allmän osäkerhetsprincip
Osäkerhetsprincipen gäller inte bara för position och rörelsemängd. I dess allmänna form gäller den varje par av konjugatvariabler. Två variabler är konjugerade om de åtföljande operationerna inte kommuterar. Ett exempel på ett par av konjugatvariabler är x-komponenten av impulsmoment (spinn) kontra y-komponenten av impulsmoment. Allmänt, till skillnad från fallet med position kontra rörelsemängd diskuterad ovan, beror den lägre gränsen för produkten av osäkerhet av två konjugatvariabler på tillståndet som systemet befinner sig i. Osäkerhetsprincipen gäller även de par av variabler tid och energi, men den matematiska behandlingen av detta fall skiljer sig något från operatorsmetoden nämnd ovan. Den fullständiga Heisenbergs osäkerhetsprincip är följande:
där
- A och B är observerade storheter,
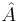 och
och 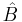 deras motsvarande operatorer,
deras motsvarande operatorer,![[\hat{A}, \hat{B}]](/w/images/sv.rilpedia.org/math/c/0/8/c081d8bf21108f8283f018b863a75393.png) betecknad kommutatorn av
betecknad kommutatorn av 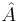 och
och 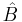 ,
,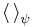 betecknar utjämning för tillståndet |ψ〉, och
betecknar utjämning för tillståndet |ψ〉, och- ΔX är standardavvikelsen av X:
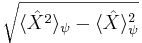 .
.
Denna relation, vilken erhålls enkelt som en konsekvens av Cauchy-Bunyakovski-Schwarz olikhet, pekades först ut 1930 av Howard Percy Robertson och (oberoende) av Erwin Schrödinger. Den är därför känd som Robertson-Schrödingerrelationen. Den kan inte bara evalueras för par av konjugerade operatorer (till exempel de som definierar mätning av distans och rörelsemängd, eller av varaktighet och energi) men allmänt för alla par av hermitiska operatorer. Det finns också en osäkerhetsrelation mellan fältstyrka och antal partiklar som är ansvariga för fenomenet virtuella partiklar.
Tolkningar
Albert Einstein accepterade inte osäkerhetsprincipen som fundamental och han utmanade Niels Bohr med ett berömt tankeexperiment: vi fyller en låda med radioaktivt material som strålar slumpmässigt. Lådan har en lucka, som öppnas och omedelbart därpå stängs av en klocka vid ett givet ögonblick, vilket medger att strålning kan slippa ut. Tiden är därmed känd med stor precision. Vi vill nu mäta konjugatvariabeln energi exakt. Enkelt enligt Einstein: bara väg lådan före och efter. Ekvivalensen mellan massa och energi från speciella relativitetsteorin låter oss beräkna precis hur mycket energi som finns kvar i lådan. Bohr bemötte: skulle energi lämna lådan, då skulle den därmed lättare lådan ge utslag på vågen, vågskålen skulle höjas. Därmed befinner sig klockan i ett område med lägre gravitationell fältstyrka och enligt den speciella relativitetsteorin kommer dess mätning av tid att avvika jämfört med dess mätning vid den tidigare positionen. En detaljerad analys visar att bristen på exakthet överensstämmer med Heisenbergs relation.
Inom den vida, men ej universellt, accepterade Köpenhamnstolkningen av kvantmekanik är osäkerhetsprincipen tagen att betyda att på en elementärnivå existerar inte det fysiska universumet i en deterministisk form - utan snarare som en samling sannolikheter, eller potentialer. Exempelvis, mönstret (sannolikhetsdistribution) producerat av miljontals fotoner som passerar genom en diffraktionsspalt kan kalkyleras med kvantmekanik, men varje fotons exakta bana kan inte förutsägas med någon känd metod. Köpenhamnstolkningen menar att den inte kan förutsägas med någon metod.
Einstein var övertygad om att denna tolkning var fel, vilket han bland annat yttrade i ett brev till Max Born 1926: "Teorin ger mycket, men den leder oss knappast närmare den Gamles hemligheter. Jag, åtminstone, är övertygad om att han inte spelar tärning." Bohr, som var en av upphovsmännen till Köpenhamnstolkningen lär ha svarat: "Tala inte om för Gud vad han ska göra!" Einsteins inställning var i stället att kvantmekanikens sannolikhetsfördelningar uppstod ur deterministiska händelser. Sannolikhetsfördelningen för en singlad slant kan till exempel vara 49 % krona och 51 % klave. Men detta betyder inte att förutsägbarheten är begränsad. Vanlig mekanik (klassisk mekanik) kan i princip användas för att exakt bestämma hur myntet landar om krafterna som verkar på myntet är kända men utfallet av krona/klave-alternativen kan ändå anses följa en sannolikhetsfördelning. Einstein antog att det finns liknande dolda variabler som ger upphov till kvantmekanikens sannolikhetsfördelningar (se vidare EPR-paradoxen).
Bell visade att en dolda variabler-teori bryter mot lokal kausalitet, genom att partiklar i ett sammanflätat tillstånd påverkar varandra omedelbart oavsett hur stort deras rumsliga avstånd är. Gemensamt för alla dolda variabler-teorier är alltså att de inte är lokala. Denna "verkan på avstånd" kan dock inte användas för att sända information, så tidsresor är omöjliga.




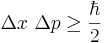
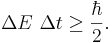
![\Delta A\,\Delta B \ge \frac{1}{2} \left|\left\langle\left[\hat{A},\hat{B}\right]\right\rangle_\psi\right|](/w/images/sv.rilpedia.org/math/8/6/4/864a27499494d8747b34c55dfc1ef912.png)