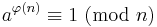Eulers sats
Från Rilpedia
Eulers sats inom talteorin säger att för positivta heltal a och n så att a och n är relativt prima så gäller
där φ(n) betecknar Eulers φ-funktion.
Satsen är en generalisering av Fermats lilla sats.
Satsen kan användas för att lättare reducera stora potenser modulo n. Betrakta till exempel problemet att hitta den sista decimalsiffran av 7222, dvs 7222 mod 10. Notera att 7 och 10 är relativt prima, och att φ(10) = 4. Eulers sats ger att 74 = 1 (mod 10), och vi får 7222 = 74·55 + 2 = (74)55·72 = 155·72 = 49 = 9 (mod 10).
Generellt när man reducerar en potens av a modulo n (där a och n är relativt prima) måste man arbeta modulo φ(n) i exponenten till a. Detta är innebörden i en alternativ formulering av Eulers sats, nämligen att om a och n är relativt prima så gäller:
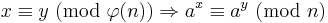
Bevis
Leonhard Euler publicerade ett bevis 1736. Satsen kan bevisas genom att använda Lagranges teorem från den abstrakta algebran. Talen a som är relativt prima med n bildar en grupp under multiplikation mod n. Detta är enhetsgruppen till ringen Z/nZ. Denna grupp har φ(n) element, och Eulers sats följer sedan från Lagranges teorem.