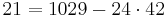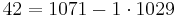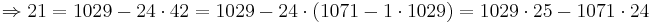Från Rilpedia

Euklides algoritm är en algoritm för att bestämma största gemensamma delare till två positiva heltal. Det är en av de äldsta kända algoritmerna och beskrivs i Euklides Elementa. Algoritmen kräver inte att man kan dela upp talen i faktorer.

Algoritmen kan beskrivas på följande sätt:

1. Två heltal a och b, där a > b är givna.
2. Om b = 0 är algoritmen klar och svaret är a.
3. I annat fall beräknas c, resten när man delat a med b.
4. sätt a = b, b = c och börja om från steg 2 igen.

Exempel 1

Finn den största gemensamma delaren till 1071 och 1029.

1) a = 1071 och b = 1029

2) (b ≠ 0)

3) 1071/1029 = 1 med 42 i rest, så c = 42

4) Sätt a = 1029, b = 42

2) (b ≠ 0)

3) 1029/42 = 24 med 21 i rest, så c = 21

4) Sätt a = 42, b = 21

2) (b ≠ 0)

3) 42/21 = 2 med 0 i rest, så c = 0

4) Sätt a = 21, b = 0;

2) b = 0, så svaret är 21

Kortare skrivet:

1071 = 1 · 1029 + 42

1029 = 24 · 42 + 21

42 = 2 · 21 + 0, så svaret är 21.

En snabb kontroll bekräftar att 1071 = 51 · 21 och 1029 = 49 · 21.

En följd av Euklides algoritm är att den största gemensamma delaren till två tal a,b kan skrivas som en linjärkombination av talen ax+by (x,y heltal). Genom att lösa ut resterna och köra algoritmen baklänges bestämmer man x och y. I exemplet ovan:

Detta kan användas vid lösning av den diofantiska ekvationen ax + by = c.

Exempel 2

Nedan följer en alternativ metod som fungerar lika bra som ovan. Med funktionen frac menas decimaldelen av talet. Om 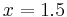så är 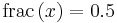och om 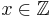, så är decimaldelen noll, dvs. .

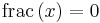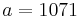
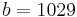
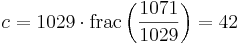
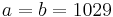
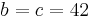
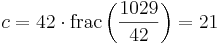
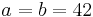
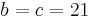
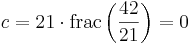
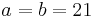
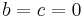
Generalisering av Euklides algoritm

Euklides algoritm kan utvidgas till att operera på andra ringar än heltalen, som ovan. Ringar i vilka Euklides algoritm kan användas kallas Euklidiska ringar. Exempel på Euklidiska ringar är de Gaussiska heltalen och vissa polynomringar.