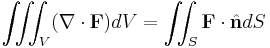Gauss sats
Från Rilpedia
I vektoranalysen är Gauss sats eller divergenssatsen ett resultat som knyter samman divergensen av ett vektorfält till värdet av flödet genom ytintegraler definierade av fältet. Gauss sats är ett viktigt resultat för fysikens matematik, till exempel elektrostatiken och flödesdynamiken. Gauss sats går även under namnet divergenssatsen.
Intuitiv uppfattning
Det intuitiva innehållet i satsen är enkelt: om det flödar vatten genom en viss region, och man är intresserad av hur mycket vatten det flödar ut ur ett specifikt område inom denna region, då måste man addera produktionen och dra av konsumtionen inom området. Vattenflödet representeras av ett vektorfält och divergensen av vektorfältet vid en given punkt beskriver styrkan av produktionen eller konsumtionen. Integrerar man fältets divergens över volymen av området borde detta vara lika med integralen av vektorfältet av områdets yta. Gauss sats säger att så är fallet.
Gauss sats är således en konserveringslag som säger att volymen av den totala produktionen eller konsumtionen, till exempel volymintegralen av divergensen, är lika med nettoflödet över volymens yta.
Formell formulering
Antag att V är en delmängd till Rn och V är kompakt och bitvis kontinuerlig och deriverbar. Om F är ett kontinuerligt, differentierbart vektorfält definierat på ett område av V så har vi att
där ytan S = ∂V är randen till området V, orienterat så att ytans normal pekar ut från ytan.
Vi noterar att Gauss sats är ett specialfall av Stokes sats, som även är en generalisering av analysens fundamentalsats.
Historia
Gauss sats upptäcktes först av Joseph-Louis Lagrange år 1762. Carl Friedrich Gauss återupptäckte den oberoende av Lagrange år 1813 och senare upptäcktes den även av George Green år 1825 och år 1831 av Mikhail Vasilievich Ostrogradsky, som också gav det första beviset till den.