Autokorrelation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Överst: sinus med brus; nederst: autokorrelation

Autokorrelationen för en stokastisk process beskriver korrelationen mellan processens olika tidpunkter.

Definition

För en tidskontinuerlig stokastisk process X definieras autokorrelationsfunktionen rX som:

r_X(t_1,t_2) = E[X(t_1)X(t_2)] \,

För en tidsdiskret stokastisk process X definieras autokorrelationsfunktionen rX som:

r_X(n_1,n_2) = E[X(n_1)X(n_2)] \,

Om autokorrelationen endast hänger av på skillnaden mellan t1 och t2 eller n1 och n2 så skrivs autokorrelationsfunktionen som:

rX(τ) = E[X(t)X(t + τ)] respektive rX(k) = E[X(n)X(n + k)]

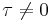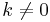Om autokorrelationen är noll för alla \tau \ne 0 eller k \ne 0 kallas X för en vit process. Fourier-transformen av autokorrelationsfunktionen kallas för effektspektrum.

Estimering

Givet en serie mätdata x_n,\ n \in [0,N-1] genererad av en svagt stationär stokastisk process X kan autokorrelationen estimeras på två sätt:

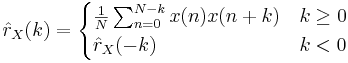
  1. icke väntevärdesriktigt: \hat{r}_X(k)=\begin{cases} \frac{1}{N} \sum_{n=0}^{N-k} x(n)x(n+k) & k \ge 0 \\ \hat{r}_X(-k) & k < 0 \end{cases}
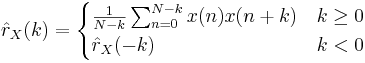
  2. väntevärdesriktigt: \hat{r}_X(k)=\begin{cases} \frac{1}{N - k} \sum_{n=0}^{N-k} x(n)x(n+k) & k \ge 0 \\ \hat{r}_X(-k) & k < 0 \end{cases}

I många sammanhang, till exempel för lösning av Yule–Walker-ekvationerna, föredras den icke väntevärdesriktiga varianten. Den väntevärdesriktiga kan då k närmar sig N anta orimligt stora värden.

Hämtad från "https://sv.rilpedia.org/wiki/Autokorrelation"
Personliga verktyg