Yule–Walker-ekvationerna
Från Rilpedia
(Omdirigerad från Yule-Walker-ekvationerna)
Yule–Walker-ekvationerna är en uppsättning ekvationer som uppstår vid skattning av parametrar för en autoregressiv modell för linjär prediktion.
Givet ekvationen
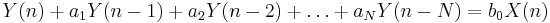 ,
,
där X(n) är vitt brus, önskas parametrarna ak beräknas. Genom att multiplicera bägge leden med Y(n − k) fås
Väntevärdet av de bägge leden blir
(rY(k) är Y:s autokorrelationsfunktion.) Men eftersom Y inte beror av framtida värden av X så är
vilket ger ekvationen
och ekvationssystemet för 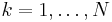 (notera att rY är symmetrisk, så rY( − k) = rY(k))
(notera att rY är symmetrisk, så rY( − k) = rY(k))
Ekvationssystem kan lösas med gausseliminering, eller, eftersom matrisen är en Toeplitz-matris, genom Levinson-rekursion.




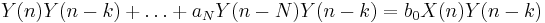
![E[Y(n) Y(n-k) + \ldots + a_N Y(n-N) Y(n-k)] = E[b_0 X(n) Y(n-k)]](/w/images/sv.rilpedia.org/math/7/c/d/7cd76e1badccd7888d9e1252b08692ea.png)
![r_Y(k) + a_1 r_Y(k-1) + \ldots + a_N r_Y(k-N)] = b_0 E[X(n) Y(n-k)]](/w/images/sv.rilpedia.org/math/c/1/e/c1e61f1c2e8cf314a032d4b60af76504.png)
![E[X(n) Y(n-k)] = 0,\ k>0](/w/images/sv.rilpedia.org/math/8/b/f/8bf0b3df72653b09f99c0523ef4b7b3a.png)
![a_1 r_Y(k-1) + \ldots + a_N r_Y(k-N)] = -r_Y(k)](/w/images/sv.rilpedia.org/math/e/c/0/ec0330f0ef07354acfa112b761986670.png)