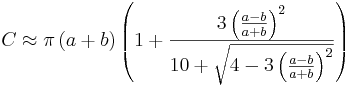Ellips (matematik)
Från Rilpedia
En ellips kan lite grovt kallas en "något tillplattad cirkel". En mer korrekt matematisk definition är att ellipsen är en geometrisk figur som motsvarar en excentrisk cirkel. Ellipsen motsvaras av ett diagonalt snitt genom en kon och kan definieras som mängden av punkter i ett plan vars sammanlagda avstånd till två givna punkter (brännpunkterna) är konstant.
Innehåll |
Konstruktion
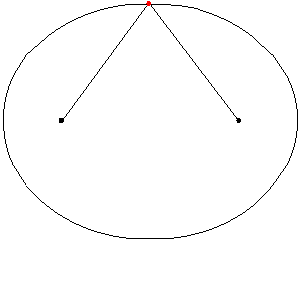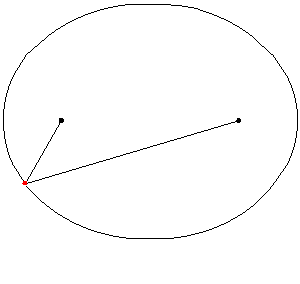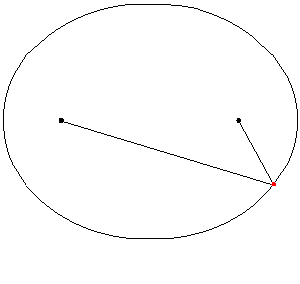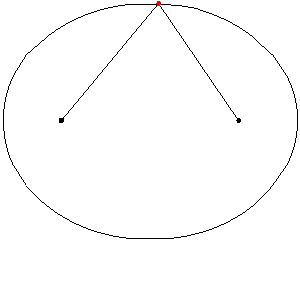
En approximation till en ellips kan ritas med hjälp av två spikar, en tråd och en penna. Spikarna placeras där man vill ha ellipsens brännpunkter. Tråden binds fast i spikarna. Den fria trådens längd ska vara lika med den önskade summan av avståndet från ellipsen till brännpunkterna. Pennan placeras så att den sträcker tråden. Pennan förs åt sidan i de riktningar för vilka trådens sträckta tillstånd bibehålls. På detta sätt kan halva ellipsen ritas. För att rita den andra halvan flyttar man pennan till andra sidan av tråden, sträcker ut tråden åt andra hållet och upprepar ritandet enligt ovan.
Egenskaper
Ellipsen definieras som orten av de punkter vars sammanlagda avstånd till brännpunkterna (F1 och F2 i diagrammet) är konstant, dvs. summan av sträckorna F1 - X och X - F2 = konstant. Denna konstant är detsamma som längden av ellipsens längre axel (AB) i diagrammet. Ofta används halva detta avstånd, den s.k. halva storaxeln, i matematiska och fysikaliska sammanhang. I astronomin betecknas halva storaxeln med bokstaven a, som i diagrammet. Lillaxeln ligger korsar vinkelrätt storaxelns mitt: halva lilla axeln betecknas b i diagrammet.
Ekvationer
där a och b > 0 (när a=b=1 är detta ekvationen för en cirkel). När ellipsen har medelpunkt i origo (h=k=0) så skär den x-axeln i punkterna (±a, 0)och y-axeln i (0, ±b).
På parameterform kan ellipsen beskrivas av
där t varierar inom intervallet 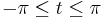 .
.
Area och omkrets
Arean av en ellips är πab där a och b är halva längden av ellipsens storaxel respektive lillaxel.
Omkretsen av en ellips kan inte uttyckas med elementära funktioner då a och b är olika utan ges av en s.k. eliptisk integral. Uttryckt som en oändlig potensserie kan omkretsen uttryckas som
En god approximation är Ramanujans:
Och en ännu bättre approximation:
Ellipsen i astronomin
Det var ett viktigt steg för människans föreställningar om universum när Johannes Kepler under det tidiga 1600-talet visade att planeternas banor kring solen är ellipser, med en av brännpunkten i solen. Keplers lagar var en stor förbättring jämfört med Ptolemaeus excentriska cirklar och epicyklar.






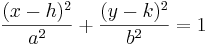
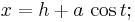
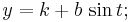
![C = 4 a E(\varepsilon) = 2\pi a \left\{1 - \left(\frac{1}{2}\right)^2 \frac{\varepsilon^2}{1} - \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 \frac{\varepsilon^4}{3}
- \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{\varepsilon^6\over5}
- \cdots - \left[\frac{\left(2n - 1\right)!!}{\left(2n\right)!!}\right]^2 \frac{\varepsilon^{2n}}{2 n-1} - \cdots \right\}\!](/w/images/sv.rilpedia.org/math/6/a/0/6a0952bf5828702bc2b6ed2ea4f486d6.png)
![C \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](/w/images/sv.rilpedia.org/math/6/a/e/6ae2da9bd47bab3bde7713c60a04c1bc.png)