Från Rilpedia

Ett integritetsområde är inom matematik en speciell algebraisk struktur, närmare bestämt en kommutativ ring med etta som saknar nolldelare, dvs att för element a och b i ett integritetsområde gäller att ab = ba = 0 implicerar a = 0 eller b = 0. Integritetsområden är specialfall av domäner, som är allmänna ringar (inte nödvändigtvis kommutativa) utan nolldelare.

Innehåll 1 Definitioner 2 Exempel 2.1 Motexempel 3 Egenskaper 4 Referenser

Definitioner

Om (R, * , + ) är en kommutativ ring med etta så är den ett integritetsområde om något av följande är uppfyllt (villkoren är ekvivalenta):

• R har inga nolldelare.
• De multiplikativa annuleringslagarna gäller: Om a är nollskilt implicerar ab = ac att b = c.
• Nollidealet {0} är ett primideal.

Exempel

• Varje kropp är ett integritetsområde.
• Heltalen 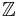är ett integritetsområde som inte är en kropp.
• En polynomring är ett integritetsområde om den är definierad över ett integritetsområde. Exempelvis är , ringen av alla polynom i en variabel med heltalskoefficienter ett integritetsområde.
• Om U är en sammanhängande öppen mängd i det komplexa talplanet så är ringen av alla analytiska funktioner 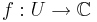ett integritetsområde.

Motexempel

• För 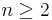är ringen av alla n×n-matriser inte ett integritetsområde.

Egenskaper

• Om R är ett integritetsområde, så finns (upp till isomorfi) en minsta kropp S som innehåller R som delring. Kroppen S kallas R:s fraktionskropp och består av element ab ^{− 1} där 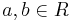och 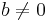. Exempelvis är fraktionskroppen till heltalen 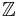de rationella talen .
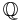• Ett integritetsområdes karakteristik kan endast vara 0 eller ett primtal.
• Om R är en kommutativ ring med ett ideal P så är kvotringen R/P ett integritetsområde om och endast om P är ett primideal.

Referenser

• Svensson, Per-Anders: Abstrakt Algebra, Studentlitteratur, 2001. ISBN 91-44-01262-4.