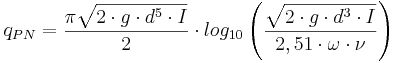Prandtl-Nikuradses formel
Från Rilpedia
Prandtl-Nikuradses formel är användbar vid turbulent flöde under hydraulisk glatta förhållanden. Formeln är uppkallad efer Ludwig Prandtl och Johann Nikuradse. För cirkulärt fullgående rör ser formeln ut enligt följande:
där
qPN = Flöde (m3)
π = Matematisk konstant (3,14159...)
g = Tyngdaccelerationen (m/s2)
d = Innerdiameter (m)
I = Fall (-)
ω = Empiriskt vågighetstal (-)
ν = Kinematisk viskositet (m2)
Friktionstal
Prandtl-Nikuradses formel kan även användas för att uttrycka friktionstalet i Darcy-Weisbachs ekvation. Då ser ekvationen ut på följande sätt:
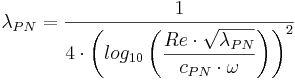 Implicit form
Implicit form
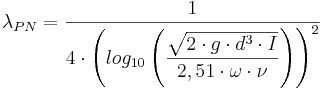 Explicit form
Explicit form
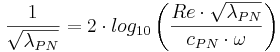 Implicit form
Implicit form
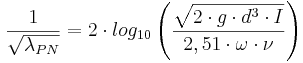 Explicit form
Explicit form
där
λPN = Friktionstal (-)
Re = Reynolds tal (-)
cPN = Empirisk konstant (2,51)
g = Tyngdacceleration (m/s2)
d = Innerdiameter (m)
I = Fall (-)
ω = Empiriskt vågighetstal (-)
ν = Kinematiskt viskositet (m2/s)
Det empiriska vågighetstalet
| Rörtyp | Vågighetstal |
|---|---|
| Perfekt glatta rör av t.ex. glas | 1,0 |
| Släta, oslitsade plaströrsledningar | 1,0-1,2 |
| Släta, slitsade plaströrsledningar | 1,1-1,4 |
| Släta vällagda betongledningar | 3-5 |
| Släta vällagda tegelrörsledningar | 4-8 |