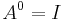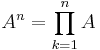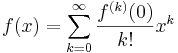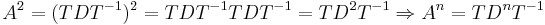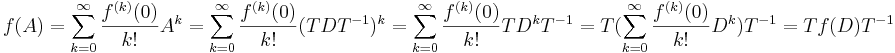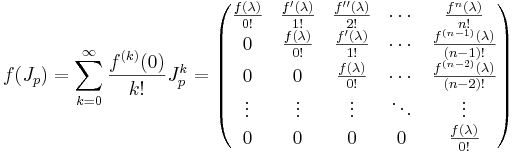Matrisfunktion

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematiken är en matrisfunktion en funktion som avbildar en matris på en matris.

Innehåll

Enkla matrisfunktioner

En del funktioner på skalärer är lätta att överföra till kvadratiska matriser., t.ex. polynomfunktioner. Med matrismultiplikation definierar man

A^0 = I \,
A^n = \prod_{k=1}^nA

för att på så sätt kunna hantera polynom av matriser. Men de flesta funktioner är inte lika enkla att överföra till matriser.

Skalärfunktioner överförda till matriser

Det finns flera aspeketer när man betraktar överföringen av en funktion från skalärer till matriser.

Maclaurinutveckling

En funktions Maclaurinserie:

f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}x^k

kan även användas på matriser.

Funktioner av diagonaliserbara matriser

För en diagonalmatris D kan man genom Maclaurinserien få att:

f(D) = \begin{pmatrix} f(d_1) & 0 & \cdots & 0 \\ 0 & f(d_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & f(d_n) \end{pmatrix}

Om en matris A är diagonaliserbar, dvs det finns en matris T sådan att A = TDT − 1, brukar man använda faktumet att:

A^2 = (TDT^{-1})^2 = TDT^{-1}TDT^{-1} = TD^2T^{-1} \Rightarrow A^n = TD^nT^{-1}

Maclaurinserien ger då att:

f(A) = \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}A^k = \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}(TDT^{-1})^k = \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}TD^kT^{-1} = T(\sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}D^k)T^{-1} = Tf(D)T^{-1}

Funktioner av matriser på Jordans normalform

Alla kvadratiska matriser kan skrivas på Jordans normalform, dvs A = TJT − 1 där J är en blockdiagonal matris. På samma sätt som för diagonala matriser får man att:

f(A) = Tf(J)T − 1

För att definiera matrisen för J kan man avnända faktumet att J = D + N för en diagonalmatris D och en nilpotent matris N, detta kan göras exempelvis i fallet matrisexponential.

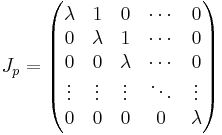
Man kan också betrakta funktioner av Jordanblock, som är de block som matrisen J har i sin diagonal. Ett Jordanblock Jp har formen:

J_p = \begin{pmatrix} \lambda & 1 & 0 & \cdots & 0 \\ 0 & \lambda & 1 & \cdots & 0 \\ 0 & 0 & \lambda & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \lambda \end{pmatrix}

Dvs, en matris med ett tal λ i huvuddiagonalen, med en diagonal av ettor ovanför huvuddiagonalen. Funktionen av ett Jordanblock blir då:

f(J_p) = \sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!}J_p^k = \begin{pmatrix} \frac{f(\lambda)}{0!} & \frac{f'(\lambda)}{1!} & \frac{f''(\lambda)}{2!} & \cdots & \frac{f^n(\lambda)}{n!} \\ 0 & \frac{f(\lambda)}{0!} & \frac{f'(\lambda)}{1!} & \cdots & \frac{f^{(n-1)}(\lambda)}{(n-1)!} \\ 0 & 0 & \frac{f(\lambda)}{0!} & \cdots & \frac{f^{(n-2)}(\lambda)}{(n-2)!} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \frac{f(\lambda)}{0!} \end{pmatrix}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Matrisfunktion"
Personliga verktyg
På andra språk