Venndiagram
Från Rilpedia
Venndiagram är illustrationer som används i mängdlära för att visa på det matematiska eller logiska sambandet mellan klasser eller mängder. Vanligen, men inte nödvändigtvis (se nedan), består ett Venndiagram av två eller tre överlappande cirklar och hanterar tre respektive sju möjliga kombinationer.
Venndiagram har fått sitt namn efter den brittiske logikern John Venn (1834-1923) och har många praktiska tillämpningar inom till exempel logik och statistik.
Ett Venndiagram innehåller alltid alla kombinationer mellan mängder som är logiskt möjliga och kan därför användas till informella bevis. Andra typer av liknande diagram, till exempel Eulerdiagram och Johnstondiagram, kan användas för att illustrera en specifik logisk sats, till exempel "A men inte B".
I ett Venndiagram som innehåller de tre mängderna A, B och C måste varje punkt (som representerar ett element) höra till någon av kategorierna:
- punkten ligger varken i A, B eller C
- punkten ligger i antingen A, B eller C
- punkten hör till exakt två mängder
- punkten hör till alla tre mängder
Innehåll |
Exempel
I Venndiagrammet till höger kan den orange cirkeln (mängd A) få representera alla tvåbenta djur och den blå (mängd B) alla djur som kan flyga.
- I snittet, det område där de två mängderna överlappar varandra, finns då alla djur som både har två ben och kan flyga (till exempel en papegoja).
- Unionen mellan mängderna, det område som upptas av båda cirklarna, representerar då alla djur antingen kan flyga eller som har två ben eller både och.
- I mängden A finns djur som har två ben men inte kan flyga, till exempel människan, och i B djur som kan flyga men inte är tvåbenta, till exempel myggor.
"Univers"
Ibland kan en rektangel som tänks representera ett "univers" läggas till Venndiagrammet. Genom att definiera detta univers kan man visa om ett element ingår i unionen, (2) ingår i universumet eller (3) helt saknar relevans.
Om man således definierar detta univers som "djur":
- Till exempel spindlar och valar som varken är tvåbenta eller kan flyga utanför unionen av A och B.
- Utanför universumet faller till exempel träd som ju överhuvudtaget inte är djur.
Eulerdiagram är inte Venndiagram
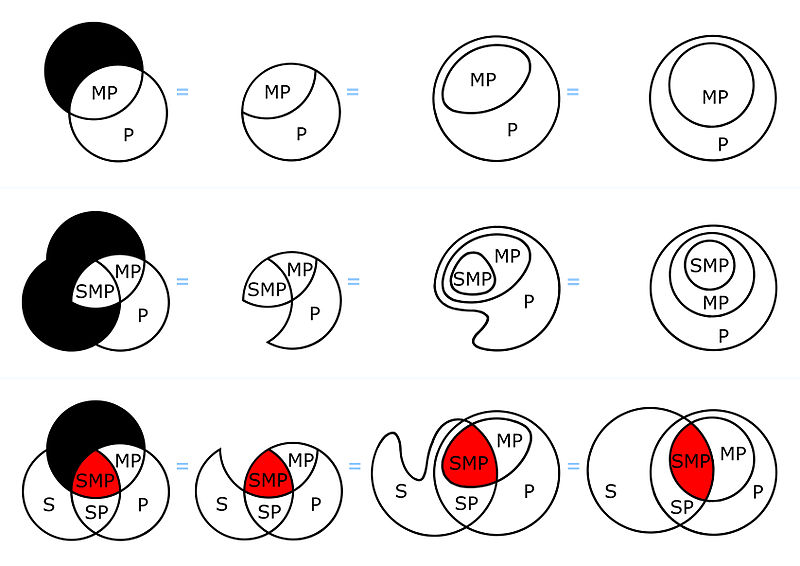
Den andra illustrationen, Eulerdiagrammet, är inte ett Venndiagram eftersom alla möjliga kombinationer inte finns representerade. Eulerdiagram kallas dock ofta slarvigt för Venndiagram. Venndiagram är en typ av Eulerdiagram.
Detta Eulerdiagram illustrerar alltså bara satsen "A är en delmängd till B men C har inga element gemensamma med B".