Från Rilpedia

Logisk operator, Logisk grind
negation, NOT konjunktion, AND, NAND disjunktion, OR, XOR, NOR implikation ekvivalens, XNOR konnektiv sanningsfunktion sanningsvärdetabell de Morgans lagar

De Morgans lagar är två vanliga regler inom logik och boolesk algebra, uppkallade efter Augustus de Morgan. Enkelt uttryckt innebär de följande:

inte (P och Q) = (inte P) eller (inte Q)

inte (P eller Q) = (inte P) och (inte Q)

Med notation från den formella logiken blir det så här:

Reglerna används även inom mängdlära:

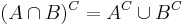
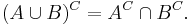
De Morgans lagar används även inom digitalteknik och programmering. I digitaltekniken skapar översättnig mellan kretsfunktioner möjligheter till optimeringar och val av tekniker. De Morgans lagar motsvaras som logiska grindar enligt (H = hög nivå, L = låg nivå):

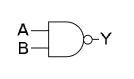=	A B A NAND B NOT-A OR NOT-B H H L L H L H H L H H H L L H H

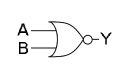= Fil:120px-AND2N-gate-US.PNG

A B A NOR B NOT-A AND NOT-B H H L L H L L L L H L L L L H H