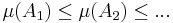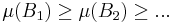Egenskaper hos mått

Från Rilpedia

Version från den 27 mars 2009 kl. 22.01 av Petter Strandmark (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Denna artikel utgör en fördjupning av artikeln om mått.

Ett mått har några intressanta egenskaper. Låt 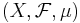(X,\mathcal{F},\mu) vara ett måttrum.

Innehåll

Grundläggande egenskaper

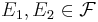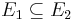Monotonicitet: Om E_1, E_2 \in \mathcal{F} där E_1 \subseteq E_2 så är

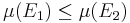\mu(E_1) \leq \mu(E_2).

Subadditiv: Om 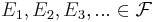E_1, E_2, E_3, ... \in \mathcal{F} är en följd av mängder (inte nödvändigtvis disjunkta) så gäller att

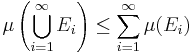\mu\left(\bigcup_{i=1}^\infty E_i\right) \leq \sum_{i=1}^\infty \mu(E_i) .

Konvergenssatser

Ett mått uppfyller följande konvergenssatser:

  • Om 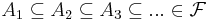A_1 \subseteq A_2 \subseteq A_3 \subseteq ... \in \mathcal{F} så är
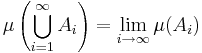\mu\left(\bigcup_{i=1}^\infty A_i\right) = \lim_{i \rightarrow \infty} \mu(A_i) .
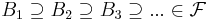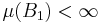  • Om B_1 \supseteq B_2 \supseteq B_3 \supseteq ...\in \mathcal{F} där \mu (B_1) < \infty så är
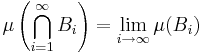\mu\left(\bigcap_{i=1}^\infty B_i\right) = \lim_{i \rightarrow \infty} \mu(B_i) .

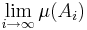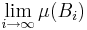Gränsvärdena \lim_{i \rightarrow \infty} \mu(A_i) och \lim_{i \rightarrow \infty} \mu(B_i) finns eftersom måttet är monotont:

\mu(A_1) \leq \mu(A_2) \leq ...
\mu(B_1) \geq \mu(B_2) \geq ...

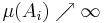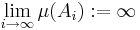om \mu(A_i) \nearrow \infty så definierar vi \lim_{i \rightarrow \infty} \mu(A_i) := \infty .

Se även

Källor

  • P. Halmos, Measure theory, D. van Nostrand and Co., 1950


Postscript-viewer-blue.svg
 Detta är en sparad artikelbok.


Måtteori

Mått (matematik)
Konstruktion av en icke mätbar mängd
Definition
Yttre mått
Egenskaper hos mått
Begrepp
Nollmängd
Nästan överallt
Fullständigt mått
Integration
Mätbar funktion
Lebesgueintegration
Egenskaper hos måttintegral
Hämtad från "https://sv.rilpedia.org/wiki/Egenskaper_hos_m%C3%A5tt"
Personliga verktyg