Additivitet
Från Rilpedia
| En eller flera användare anser att additiv funktion bör infogas i denna artikel. (Diskussion) |
Additivitet är ett begrepp inom matematiken som anger hur en funktion uppför sig vid summering. Begreppet har olika betydelser beroende på vilka slags funktioner som avses.
Det enklaste fallet är en additiv funktion, som bevarar addition:
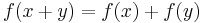 .
.
Inom måtteorin, där funktioner definierade för mängder avses, gäller följande för additivitet:
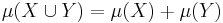 om
om 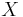 och
och 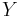 är mängder med inga gemensamma element.
är mängder med inga gemensamma element.
Subadditivitet
En funktion som definieras på mängder är subadditiv om istället
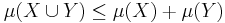 .
.
Sigma-additivitet
Definitionerna ovan kan med hjälp av induktion visas för varje ändlig summa av längd n:
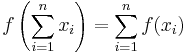 ,
,
respektive
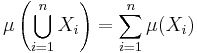 .
.
Om dessa uttryck även gäller för uppräkneliga summor (vilket inte alltid är fallet) kallas egenskapen sigma-additivitet eller σ-additivitet.
Referenser
- G. B. Folland, Real Analysis: Modern Techniques and Their Applications, John Wiley and Sons 1999 ISBN 0-471-317160-0



