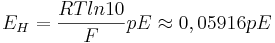pE (måttenhet)

Från Rilpedia

Version från den 19 december 2008 kl. 14.30 av Sjunnesson (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

pE är ett logaritmiskt mått på elektronaktiviteten i en kemisk lösning (t ex markvätska). Höga pE-värden indikerar oxiderande förhållanden med god tillgång på syrgas och låg elektronaktivitet. Låga pE-värden indikerar reducerande förhållanden, med frånvaro av syrgas (syrgasbrist) och hög elektronaktivitet.

Strikt matematiskt definieras pE som den negativa 10-logaritmen av elektronaktiviteten, d v s pE = -log10(e-) där (e-) är elektonaktiviteten. pE är matematiskt kopplad till elektrodpotentialen (EH) genom sambandet EH = 0,05916 pE.


Innehåll

Olika redoxförhållanden

Inom markkemin brukar man skilja på oxiska, suboxiska och anoxiska förhållanden. Vid oxiska förhållanden är pE över 7 och syrgas finns att tillgå för biokemiska reaktioner. Vid suboxiska förhållanden är pE 2-7 har syrgasen tagit slut. Vid anoxiska förhållanden är pE lägre än +2. Dessa gränsvärden gäller vid pH 7. Vid lägre pH-värden får pE-gränserna justeras uppåt och vid högre pH-värden fär pE-gränserna justeras neråt.

Ibland används bara uttrycken oxiderande förhållanden och reducerande förhållanden, där oxiderande förhållanden råder vid höga pE-värden och reducerade förhållanden råder vid låga pE-värden.

pE-pH diagram

Då nästan alla redox-reaktioner i markvätskan påverkas av (och påverkar) dess pH-värde, är det ofta lämpligt att göra ett s.k. pE-pH-diagram för relevanta grundämnen. I pE-pH-diagrammet framgår tydligt vilka kemiska former av t.ex. järn, mangan eller svavel som dominerar vid en given kombination av pE och pH. Ofta plottas pH på x-axeln och pE på y-axeln.


Det matematiska sambandet mellan pE och pH

Om vi tänker oss den allmänna redox-reaktionen

mAox + nH+ + e- \rightleftharpoons pAred + qH20

så blir jämviktskonstanten (K)

K = \dfrac{A_{red}^p (H_2O)^q}{(A_{ox})^m (H^+)^n (e^-)} \approx \dfrac{A_{red}^p}{(A_{ox})^m (H^+)^n (e^-)}

då vattenaktiviteten (H2O) brukar kunna sättas till 1. Om uttrycket för K logaritmieras, får vi

log K = p*log (Ared) - m*log (Aox) - n* log (H+) - log (e-)

Då pH = -log (H+) och pE = -log (e-), får vi

log K = p*log (Ared) - m*log (Aox) + n*pH + pE

var på pE kan lösas ut

pE = log K + m*log (Aox) - p*log (Ared) - n*pH

Om både den reducerade formen (Ared) och den oxiderande formen (Aox) är vattenlösliga, inträffar jämviktsläget mellan de olika formerna när

p*log (Ared) = m*log (Aox)

varpå sambandet mellan pE och pH kan förenklas till

pE = log K - n*pH

Det är detta samband som ritas ut på pE-pH diagrammet.

Att mäta pE och pH i markvätskan

Både pE och pH mäts på liknande sätt, varför bägge mätningarna tas upp här.

Att mäta pE

Om redoxreaktionen sker i en vattenlösning, kan pE mätas med hjälp av elektroder. Man nyttjar då sambandet mellan pE och elektrodpotentialen:

E_H = \dfrac {R T ln 10}{F} pE \approx 0,05916 pE

där

EH = Elektrodpotential (V)

R = Allmänna gaskonstanten (8,314 4 J/(K mol))

T = Temperatur (298 K)

F = Faradays konstant (96 486 C/mol)

Om man använder en ren platina-elektrod tillsammans med en kalomel-elektrod (kalomel = Hg2Cl2), så oxideras platinan, och kalomelen reduceras enligt följande halvreaktion:

1/2 Hg2Cl2(s) + e- \leftrightharpoons Cl-(aq) + Hg*(l) (log K = 4,53).

Med tillämpning av termodynamikens lagar, kan man beräkna elektrodpotentialen mellan två elektroder kan genom formeln:

E = B + Ej + EH = B + Ej + 0,05916(pE)

där

B = en parameter som beror på log K. B är unik för varje kalomelelektrod.

Ej = "vätskekopplingspotentialen" i en saltbrygga bestående av mättad lösning av kaliumklorid (som hindrar kloridjonerna från att diffundera ut från kalomel-elektroden). Ej beror på rådande jämviktförhållanden i saltbryggan.

Det sammanlagda värdet av B + Ej fås genom kalibrering av elektroderna mot olika redox-buffertar med kända egenskaper, t ex en blandning av 0,1 M järn(II)sulfat + 0,1 M Fe(III)sulfat i en 1 M svavelsyra.

Praktiska problem med pE-mätning i markvätskan

Det finns ett fleral praktiska problem med att mäta pE-värdet i markvätskan:

  1. Platinaelektroden svarar på flera halvreaktioner, utöver kalomel-elektroden.
  2. Koncentrationen av många redoxämnen är för låg i markvätskan, för att kunna påverka platinaelektroden.
  3. Vissa redoxämnen (t ex sådana ämnen som reducerar kol, kväve och svavel) är inte elektroaktiva.
  4. Platinaelektroden kontamineras av oxider och andra föroreningar.
  5. Ej i markvätskan skiljer sig rejält från Ej i redoxbufferten.

En pE-mätning ger bara ett kvalitativt mått på markens redoxpotential. Det uppmätta pE-värdet duger bara till att typkategorisera marken som oxisk, suboxisk eller anoxisk.

pH-mätning

Om kalomelelektroden behålls oförändrad, medan man byter ut pE-mätarens platinaelektrod mot en glasmembranelektrod, får man en pH-mätare. Glasmembranet fungerar som en adsorbtionsyta för markvätskans protoner. Den pH-skillnad som finns mellan markvätska och glasmembranets innervätska skapar en mätbar elektrodpotential. Sambandet mellan pH och elektrodpotentialen ser ut på följande sätt:

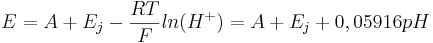
E = A + E_j - \dfrac {R T}{F} ln (H^+) = A + E_j + 0,05916 pH

där

E = Elektrodpotential mellan två elektroder (V)

A = en parameter som beror på log K. A är unik för varje kalomel elektrod.

Ej = "vätskekopplingspotentialen" i en saltbrygga bestående av mättad lösning av kaliumklorid (som förhindrar kloridjonerna från att diffundera ut från kalomel-elektroden). Ej beror på de rådande steady-state förhållandet i saltbryggan.

R = Allmänna gaskonstanten (8,3144 J/(K mol))

T = Temperatur (298 K)

F = Faradays konstant (96486 C/mol)

(H+) = vätejons-aktiviteten

När det gäller proton-aktivitet, sker kalibreringen direkt mot buffertlösning med känt pH-värde. Därför mäts bara relativa pH-värden:

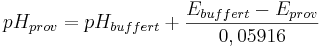
pH_{prov} = pH_{buffert} + \dfrac {E_{buffert} - E_{prov}}{0,05916}

där

pHbuffert = pH-värdet i bufferten.

pHprov = pH-värdet i det undersökta provet (markvätskan)

Ebuffert = Elektrodpotentialen i bufferten (V)

Eprov = Elektrodpotentialen i det undersökta provet (V)


Praktiska problem med pH-mätningar av markvätskan

Det principiella problemet med pH-mätningar i markvätskan är osäkerheten i vätskekopplingspotentialen (Ej). Då markvätskans innehåll skiljer sig radikalt från pH-buffertens innehåll, så kommer vätskekopplingspotentialen att förändras. Det är omöjligt att förutse hur stor skillnaden kan tänkas bli. Blir skillnaden alltför stor, så blir det uppmätta pH-värdet oanvändbart för att kunna karakterisera det kemiska tillståndet i marken.

Källor

  • Sposito, Garrison: The Chemistry of Soils, 277 sid. Oxford University press, New York 1989. ISBN 0-19-504615-3. 


Se även

Hämtad från "https://sv.rilpedia.org/wiki/PE_(m%C3%A5ttenhet)"
Personliga verktyg