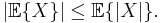Jensens olikhet

Från Rilpedia

Version från den 30 maj 2009 kl. 20.10 av ArthurBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematiken är Jensens olikhet en uppskattning av integraler av konvexa funktioner. Olikheten används ofta då man vill visa att sekvenser av funktioner konvergerar mot någon gränsfunktion eller då man är intresserad av konvergenshastigheter.

Olikheten kan ses som en generalisering till allmänna konvexa funktioner av olikheten

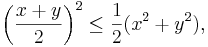
\left(\frac{x+y}{2}\right)^2 \leq \frac{1}{2} (x^2+ y^2),

giltig för reella tal x och y.

Jensens olikhet

Låt 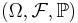(\Omega,\mathcal{F},\mathbb{P}) vara ett sannolikhetsrum och låt X vara en reell-värd stokastisk variabel på Ω. Om väntevärdet

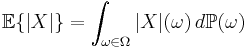
\mathbb{E}\{\vert X \vert\} = \int_{\omega \in \Omega} \vert X \vert(\omega) \, d\mathbb{P}(\omega)

är ändligt och

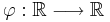
\varphi : \mathbb{R} \longrightarrow \mathbb{R}

är en konvex funktion, så gäller olikheten

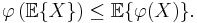
\varphi\left(\mathbb{E}\{X\}\right) \leq \mathbb{E}\{\varphi(X)\}.

Ofta tillämpar man Jensens olikhet på den konvexa funktionen 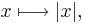x \longmapsto \vert x \vert, vilket ger olikheten

\vert \mathbb{E}\{X\} \vert \leq \mathbb{E}\{\vert X \vert\}.

Hämtad från "https://sv.rilpedia.org/wiki/Jensens_olikhet"
Personliga verktyg