Isometri
Från Rilpedia
Version från den 3 maj 2009 kl. 02.06 av Calle (Diskussion)
En isometri är inom matematiken en funktion från ett metriskt rum till ett annat, som uppfyller vissa krav.
En funktion f från ett metriskt rum (X,dX) till ett annat metriskt rum (Y,dY) säges vara en isometri om den är avståndsbevararande, dvs
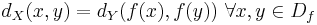 .
.
En linjär avbildning från ett normerat rum till ett annat normerat rum, 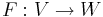 , sägs vara en linjär isometri om den bevarar normen:
, sägs vara en linjär isometri om den bevarar normen:
då 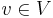 och
och 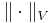 och
och 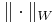 är normerna i V respektive W..
är normerna i V respektive W..
Exempel
I det Euklidiska planet utgörs alla isometrier av identitetsavbildningen, translationer, rotationer, speglingar och glidspeglingar. I detta fall gäller
Allmänt är alla ortogonalmatriser och unitära matriser isometrier. Alla isometrier mellan ett vektorrum bildar den euklidiska gruppen. Alla linjära isometrier bildar ortogonalgruppen.