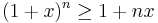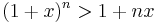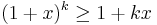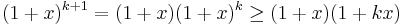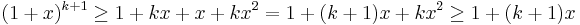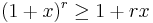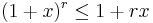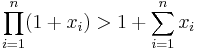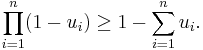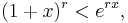Bernoullis olikhet
Från Rilpedia
Bernoullis olikhet, efter Jakob Bernoulli, är en matematisk olikhet som approximerar exponentiering av 1+x. den används ofta i bevis av andra olikheter.
Olikheten lyder
för varje heltal n ≥ 0 och varje reellt tal x > −1. Om exponenten n är jämn gäller olikheten för alla reella tal x. En strikt variant av olikheten lyder
för varje heltal n ≥ 2 aoch varje reellt tal x ≥ −1 med x ≠ 0.
Innehåll |
Bevis
Olikheten kan bevisas med hjälp av induktion: För n=0, 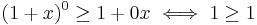 vilket är sant.
vilket är sant.
Antag nu att olikheten gäller för n=k:
Då gäller att
(från antagandena, då 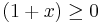 ), så
), så
(då 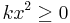 ) Detta ger att
) Detta ger att 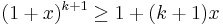 , vilket bevisar att antagandet även gäller för n=k+1.
, vilket bevisar att antagandet även gäller för n=k+1.
Induktion ger nu att olikheten gäller för alla 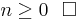
Generaliseringar
Exponenten n kan generaliseras till ett godtyckligt reellt tal r enligt följande: om x > −1, så är
om r ≤ 0 eller r ≥ 1, och
för 0 ≤ r ≤ 1. Generaliseringen kan visas genom jämförelser av derivatorna. Återigen kräver den strikta varianten av olikheterna att x ≠ 0 och att r ≠ 0, 1.
Man kan även generalisera olikheten till godtyckliga faktorer:
om 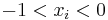 gäller för all
gäller för all 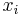 eller
eller 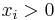 för alla
för alla 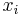 . Detta bevisas på motsvarande sätt som induktionsbeviset ovan.
. Detta bevisas på motsvarande sätt som induktionsbeviset ovan.
Om man låter 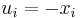 och
och 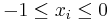 (med andra ord
(med andra ord 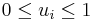 ), Så får man Weierstrass produktolikhet:
), Så får man Weierstrass produktolikhet:
Besläktade olikheter
Följande olikhet begränsar 1 + x upphöjt til r uppåt. För alla reella tal x, r > 0 gäller
där e är basen för naturliga logaritmen Detta kan visas genom att använda olikheten (1 + 1/k)k < e.
Källor
- Artikeln är, helt eller delvis, en översättning från engelskspråkiga Wikipedia.
- Artikeln är, helt eller delvis, en översättning från tyskspråkiga Wikipedia.