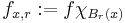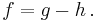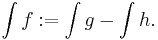Integrerbarhet
Från Rilpedia
Integrerbarhet är en matematiskt begrepp inom integrationsteori. Det finns många definitioner för integrerbara funktioner och det är beroende av vilken integralen man användar.
Innehåll |
Riemannintegrerbarhet
- Se även: Riemannintegration
Riemannintegrerbarhet är, lite förenklat, att man kan stänga in grafen till funktionen f mellan två trappstegsfunktioner där den ena trappan hela tiden är ovanför funktionsgrafen och den andra trappan är nedanför.
För att definiera integrerbarhet används två trappstegsfunktioner. Trappstegsfunktionerna har egenskapen att de är konstanta på särskilda så kallade trappstegsintervall. En funktion f är integrerbar om det existerar två trappstegsfunktioner g och h så att 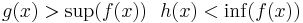 för varje x i trappstegsintervallet, oavsett hur litet intervallet är.
för varje x i trappstegsintervallet, oavsett hur litet intervallet är.
När sedan trappstegsintervallet går mot noll kommer dessa trappor att närma sig varandra och grafen till funktionen. Arean av den yta som begränsas av trappstegsfunktionerna kan lätt beräknas genom att summera arean av de rektanglar som utgör denna area. De båda summorna för trappstegsfunktionerna kommer vid gränsövergången där trappstegsintervallet går mot noll att konvergera mot varandra. Summan av dessa oändligt små men oändligt många element kallas för en Riemannsumma och definieras vara värdet på en funktionens integral.
Lebesgueintegrerbarhet
- Se även: Lebesgueintegration
Lebesgueintegrerbarhet eller med andra ord måttintegrerbarhet är ganska annorlunda från Riemannintegrerbarheten. Man definierar först måttintegralen endast för mätbara funktioner som inte har några negativa värden. Å andra sidan vill man ofta integrera funktioner som har negativa värden. Men man kan inte definiera måttintegralen för alla mätbara funktioner som har negativa värden. Så att man definiera (Lebesgue)integrerbara funktioner, dvs funktioner vars absolutbelopp är ändlig. Mer precist, om 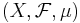 är ett måttrum och f är en mätbar funktion
är ett måttrum och f är en mätbar funktion 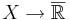 så är f integrerbar om
så är f integrerbar om
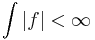 .
.
Detta kan tyckas lite konstigt, den naturliga definitionen borde vara att en integral för en mätbar funktion 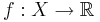 är
är
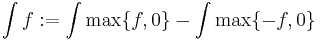 .
.
Tyvärr finns det problem med den här definitionen. Till exempel, om 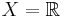 och
och 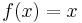 för
för 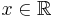 så är
så är
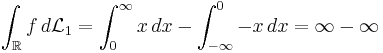 ,
,
vilket inte är definierat. Detta betyder att vi inte kan integrera alla mätbara funktioner. Vi måste betrakta en mindre klass av funktioner, som inte stöter på sådana här obestämda uttryck. Den naturliga klassen är integrerbara funktioner eftersom för integrerbara funktion har man
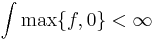 och
och 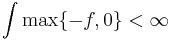 .
.
Därför är integralen för integrerbara 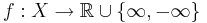 :
:
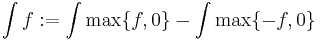 .
.
Kvasi-integrerbar
- Huvudartikel: Kvasi-integrerbar funktion.
Det finns funktioner som inte är integrerbar men är kvasi-integrebara. En funktion f är kvasi-integrerbar, om
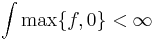 eller
eller 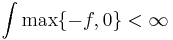 .
.
Lokalt integrebar
- Huvudartikel: Lokalt integrerbar funktion.
Det finns funktioner som är inte integrerbar men är lokalt integrebar. Om X är ett metriskt rum så är en funktion f är lokalt integrerbar om funktionen
är integrerbar för alla 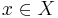 och
och 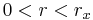 där
där 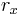 beror på punkten x.
beror på punkten x.
Lokalt integrerbara funktioner har många tillämpningar inom harmonisk analys och funktionalanalys.
p-integrerbar
- Huvudartikel: Lp-rum.
Man kan definiera en funktionklass som är p-integrebar, dvs
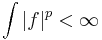 .
.
p-integrerbara funktioner studeras mycket inom funktionalanalys.
Daniellintegrerbarhet
- Se även: Daniellintegration
Daniellintegrerbarhet är ganska olika från andra integrerbarhetskoncept. Man definierar att en funktion f är integrerbar om f tillhör någon gränsfamilj för testfunktioner. Man definierar den här funktionklassen eftersom gränsfamiljer inte är sluten under subtraktion. Mer precist, om
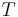 är testfunktionfamilj,
är testfunktionfamilj,
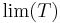 är gränsfamilj av testfunktionfamiljen och
är gränsfamilj av testfunktionfamiljen och
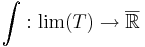 är en Daniellintegral
är en Daniellintegral
så är en funktion 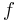 Daniellintegrerbar om det finns
Daniellintegrerbar om det finns 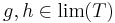 så att
så att
Man använder beteckningen 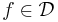 och definierar Daniellintegralen för
och definierar Daniellintegralen för 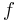 :
: