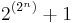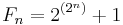Fermattal
Från Rilpedia
Version från den 5 februari 2009 kl. 07.39 av FriskoBot (Diskussion)
Fermattal kallas inom talteorin heltal av formen
där n är ett naturligt tal. Ett fermattal betecknas vanligen Fn , där
De sju första Fermattalen är (talföljd A000215 i OEIS):
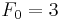
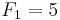
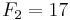
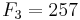
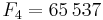
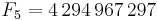
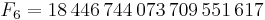 .
.
Dessa tal studerades först av Pierre de Fermat, som förmodade att alla heltal på denna form var primtal. Detta visades vara falskt av Leonhard Euler 1732 när han fann att F5 = 4 294 967 297 = 641·6 700 417. De tal på denna form som faktiskt är primtal kallas Fermatprimtal och de enda man hittills känner till är 3, 5, 17, 257 och 65537.
Alla olika Fermattal är relativt prima.