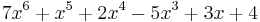Koefficient

Från Rilpedia

Version från den 10 mars 2009 kl. 16.51 av AndersBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ordet koefficient används inom bland annat matematik och fysik för att beteckna en faktor i en produkt, i sammanhang där övriga faktorer anses bestämma produktens "karaktär", medan koefficienten påverkar dess "storlek".

Innehåll

Matematik

Inom matematiken betecknar oftast en koefficient för en potens av variabeln i ett polynom det tal som man multiplicerar potensen med för att bilda motsvarande addend ("additiva term") i polynomet. Med andra ord, i polynomet

7x^6+x^5+2x^4-5x^3+3x+4\,

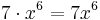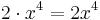är x6-koefficienten (eller sjättegradskoefficienten) 7 och x4-koefficienten (eller fjärdegradskoefficienten) 2, eftersom 7 \cdot x^6 = 7x^6\, och 2 \cdot x^4 = 2x^4\,. Vidare är x5-koefficienten 1 (trots att denna koefficient inte är explicit utskriven i uttrycket), eftersom 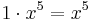1 \cdot x^5 = x^5. Tredjegradskoefficienten är -5, eftersom addenden är 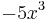-5x^3\,; förstagradskoefficienten är 3 (eftersom 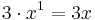3 \cdot x^1 = 3x\,), och nolltegradskoefficienten är detsamma som konstanttermen 4 (eftersom 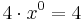4 \cdot x^0 = 4\,). Slutligen har polynomet x2-koefficienten 0, eftersom 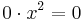0 \cdot x^2 = 0, och man alltid kan tillfoga en nollterm till en summa utan att den ändras[1]. Man bestämmer alltså koefficienterna genom att tänka sig att polynomet hade följande utseende:

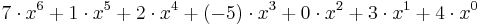7\cdot x^6 + 1\cdot x^5 + 2\cdot x^4 +(-5)\cdot x^3 + 0\cdot x^2 + 3\cdot x^1+4\cdot x^0\,.

Koefficienter förekommer också bland annat i potensserier i en variabel, i polynom och potensserier av flera variabler, och i linjärkombinationer av uppsättningar av vektorer, eller allmännare element i en given modul över en koefficientring. Detta betyder, att man kan identifiera exempelvis koefficienter i ett polynom olika, beroende på vilka faktorer man definierar som variabler och vilka som ses som möjliga delar av koefficienterna.

Ofta indexeras koefficienterna och objekten på samma sätt, vilket leder till uttryck såsom exempelvis

a0x0 + a1x1 + a2x2 + a3x3 + …

eller

a1x1 + a2x2 + a3x3 + …

där i båda fallen ai är koefficienter. Inom matematiken är inga speciella bokstäver reserverade just för koefficienter. Det inledande exemplet kan därför skrivas som exempelvis

b6x6 + b5x5 + … + b0x0

där  b0 = 4,  b1 = 3,  b2 = 0,  b3 = -5, och så vidare.

Specialfall av matematiska koefficienter är riktningskoefficienter, binomialkoefficienter, och allmännare multinomialkoefficienter.

Fysik

Inom fysiken är oftast en koefficient en fysikaliskt bestämd men sortlös faktor. Till skillnad från i matematiskt språkbruk förekommer oftast bara en koefficient av ett visst slag i ett enkelt fysikaliskt uttryck; och koefficienter med en viss fysikalisk betydelse brukar oftast betecknas med samma bokstav (möjligen försedd med index, om flera koefficienter av denna betydelse förekommer i ett sammansatt fysikaliskt uttryck).

Några exempel på fysikaliska koefficienter är brytningsindex (betecknade med n), friktionskoefficienter (betecknade med μ), utvidgningskoefficienter (betecknade med α), och temperaturkoefficienter (som också kan betecknas med α).

Övrigt

Wiki letter w.svg  Detta korta avsnitt behöver utökas.

Även inom andra områden där matematiska modeller tillämpas (som inom ekonomiska vetenskaper) talas om koefficienter.

Referenser

  1. ↑ Se Neutralt element

Se även

Aerodynamiska koefficienter


E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Stylised Lithium Atom.svg Denna artikel om fysik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Koefficient"
Personliga verktyg