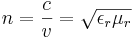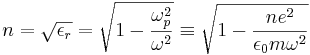Brytningsindex
Från Rilpedia
Brytningsindex, även kallat refraktionsindex, är en materialegenskap som beskriver utbredningen av elektromagnetiska vågrörelser i ett ämne.
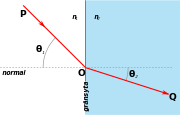
När en våg går snett från ett medium till ett annat med olika brytningsindex medför hastighetsändringen en ändring av utbredningsriktningen, där vinkeln bestäms av skillnaden mellan brytningsindex i medierna. Ändringen i brytningsindex kan vara språngartad, t ex gränsytan mellan vattnet i en sjö och luften. Men det finns också fall där brytningsindex ändrar sig kontinuerligt, t ex inom en luftmassa, där temperatur och tryck ändras långsamt utefter vågens utbredning.
Definition:
där n är brytningsindex, c ljushastigheten i vakuum och v utbredningshastigheten i det aktuella ämnet, εr är relativa permittiviteten och μr relativa permeabiliteten.
Innehåll |
Frekvensberoende
Brytningsindex är frekvensberoende (dispersion). Om inget annat sägs, avses gult natriumljus (Fraunhoferska dubbellinjen D, 589 nm) samt normal temperatur (20 °C) och tryck (1033 hPa) (NTP).
Frekvensberoendet utnyttjas bland annat för att skapa ett färgspektrum med hjälp av ett prisma. Vitt ljus faller snett in mot en yta, och bryts då in mot materialet, så att olika färg får olika riktning. Det lämnar sedan materialet genom en yta som inte är parallell med den första, så att rikningen fortfarande är olika för olika färger. När ljuset fångas på en skärm en bit bort från prismat, finns allt rött ljus i ena änden och allt violett i andra.
För en metall, där relativa permeabiliteten är ungefär 1, är brytningindex för små vinkelfrekvenser ω ungefär lika med
där ωp är plasmonfrekvensen, n är elektrontätheten, e elektronens laddning, m dess massa och ε0 permittiviteten i vakuum.[1]
Tillämpningar
Några praktiska exempel där brytningsindex spelar in:
- Refraktion: ett sugrör i ett dricksglas med vatten synes vara knäckt vid vätskeytan, trots att sugröret bevisligen är alldeles rakt. Orsaken är att vatten har annat brytningsindex än luft.
- Hägringsfenomenet beror på att atmosfären är skiktad i lager med olika brytningsindex, vilket är en följd av språngvisa ändringar av temperatur, barometerstånd, fuktighet m m.
- Radiovågors avböjning i jonosfären p g a skiktning med olika täthet av joner och fria elektroner. Denna avböjning är förklaringen till att långdistanskommunikation med kortvåg är möjlig.
- Uppkomsten av s k radaränglar, liknande mekanism som vid hägringar vid synligt ljus, fast i detta fall med radiovågor.
Brytningsindex för några material
| Vakuum | 1 (exakt) |
| Luft | 1,00029 |
| Kvävgas | 1,00030 |
| Syrgas | 1,00027 |
| Vatten | 1,33 |
| Etylalkohol | 1,36 |
| Bergkristall | 1,46 |
| Terpentin | 1,47 |
| Kronglas | 1,51 |
| Flintglas | 1,75 |
| Diamant | 2,47 |
| Titandioxidkristall | 3 |
Se även
Källor
- ↑ Kittel, Charles: Introduction to Solid State Physics, 2005. ISBN 0-471-68057-5.