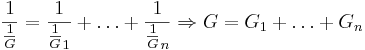Konduktans

Från Rilpedia

Version från den 16 februari 2009 kl. 17.52 av Ghostrider (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Konduktans, elektrisk ledningsförmåga, reciproken av resistansen R.

Konduktans betecknas med bokstaven G och mäts med enheten siemens S. 1 S = 1 Ω^-1.

Ibland kan konduktans (företrädesvis i USA) betecknats Mho med symbolen ℧.

Konduktansen kan beskrivas matematiskt som:

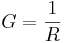$G = \frac{1}{R}$ och resistansen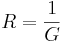 $R = \frac{1}{G}$

Tillsammans med Ohms lag för resistans 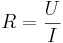$R = \frac{U}{I}$ , kan man härleda följande formel:

$I = G \cdot U \Rightarrow$ "Siemens lag" eller Ohms lag för ledningsförmåga.

Konduktivitet (ledningsförmåga)

Precis som resistiviteten i en ledare, kan man även beskriva en ledares ledningsförmåga, konduktivitet. Konduktivitet är reciproken av resistivitet.

Konduktivitet betecknas med den grekiska bokstaven σ sigma.
Resistivitet betecknas med den grekiska bokstaven ρ rho.

Matematisk kan man skriva förhållandet:

$\sigma = \frac{1}{\rho}$ och $\rho = \frac{1}{\sigma}$

En ledares konduktans och konduktivitet erhålls därför:

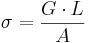
$G = \frac{\sigma \cdot A}{L}$ och $\sigma = \frac{G \cdot L}{A}$

Där A ledarens tvärsnittsarea och L är ledarens längd.

Seriekoppling av konduktanser

Beräkning av en seriekoppling med konduktanser kan beskrivas med följande härledning:

Det totala motståndet i en seriekoppling är: 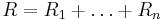$R = R_1 + \dots + R_n\,$ .

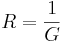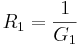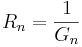Sätter man in: $R = \frac{1}{G}$ , $R_1 = \frac{1}{G_1}$ och $R_n = \frac{1}{G_n}$ i formeln, härleds en matematisklag för seriekoppling av konduktanser:

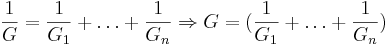$\frac{1}{G} = \frac{1}{G_1}+ \dots + \frac{1}{G_n} \Rightarrow G = (\frac{1}{G_1}+ \dots + \frac{1}{G_n})$ ^-1

Parallellkoppling av konduktanser

Beräkning av en parallellkoppling med konduktanser kan beskrivas med följande härledning:

Det toala motståndet i en parallellkoppling är: 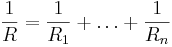$\frac{1}{R} = \frac{1}{R_1}+ \dots + \frac{1}{R_n}$ .

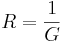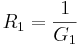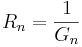Sätter man in: $R = \frac{1}{G}$ , $R_1 = \frac{1}{G_1}$ och $R_n = \frac{1}{G_n}$ i formeln, härleds en matematisklag för parallellkopplingav konduktanser:

$\frac {1}{\frac 1 G} = \frac {1}{\frac 1 G_1} + \dots + \frac {1}{\frac 1 G_n} \Rightarrow G = G_1 + \dots + G_n\,$

Denna elektricitetsrelaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.

Konduktans

Från Rilpedia

Konduktivitet (ledningsförmåga)

Seriekoppling av konduktanser

Parallellkoppling av konduktanser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk