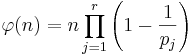Eulers fi-funktion

Från Rilpedia

Version från den 26 maj 2009 kl. 19.59 av LA2-bot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
De tusen första värdena av φ(n)

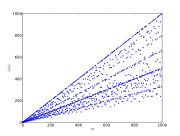
Eulers φ-funktion φ(n), namngiven efter Leonhard Euler, är en viktig aritmetisk funktion inom talteorin.

Om n är ett positivt heltal, då definieras φ(n) som antalet positiva heltal mindre än eller lika med n som är relativt prima med n. Till exempel är φ(8) = 4 eftersom de fyra talen 1, 3, 5 och 7 är relativt prima till 8.

φ är en multiplikativ funktion då m och n är relativt prima dvs φ(mn) = φ(m) φ(n).

Värdet av φ(n) kan därför beräknas genom att använda aritmetikens fundamentalsats dvs om 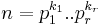n = p_1^{k_1}..p_r^{k_r} där pj är distinkta primtal, då är

\varphi(n) = n \prod_{j=1}^r \left(1 - \frac{1}{p_j} \right)

Värdet av φ(n) är lika med ordningen av enhetsgruppen till ringen Z/nZ (se modulär aritmetik). Detta tillsammans med Lagranges teorem, ger ett bevis för Eulers sats.

Egenskaper hos φ(n)

∑ φ(d) = n
d | n,d > 0
Hämtad från "https://sv.rilpedia.org/wiki/Eulers_fi-funktion"
Personliga verktyg