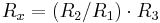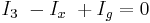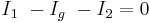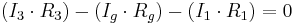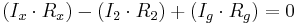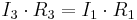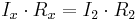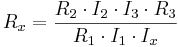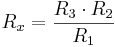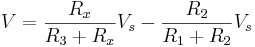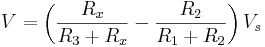Wheatstones brygga

Från Rilpedia

Texten från svenska Wikipedia

Wheatstones brygga, uppfunnen av Charles Wheatstone, är en metod att koppla tre kända och ett okänt motstånd över en galvanometer för att med stor noggrannhet bestämma det okända motståndet. Då det med metoden också går att detektera mycket små variationer i det fjärde motståndet, används den ofta i tillämpningar där det fjärde motståndet utgör en sensor som reagerar på någon yttre fysikalisk storhet.

Historia

Den ursprungliga teorin var ett hugskott av den brittiske fysikern Samuel Hunter Christie, som han publicerade 1833 som sin "diamantmetod". Wheatstone förbättrade metoden 1843, och blev känd som metodens uppfinnare. Senare utvidgade James Clerk Maxwell metoden för tillämpning också i växelströmskretsar.

Teori

kopplingsschema för Wheatstones brygga

1. Galvanometern V_G visar spänningen mellan punkterna D och B. Om R₁ och R₃ är kända, och R₂ är en potentiometer, alltså variabelt, så kan R_x bestämmas enligt formeln

$R_x = (R_2 / R_1) \cdot R_3$

Då galvanometern visar = 0.

2. Om R₂ är fast, kan Kirchhoffs lagar tillämpas för att bestämma R_x, mätande strömmen genom galvanometern.

Först bestäms strömmarna i punkterna B och D, enligt Kirschhoffs första lag:

$I_3 \ - I_x \ + I_g = 0$

$I_1 \ - I_g \ - I_2 = 0$

Därefter, enligt Kirchhoffs andra lag, bestäms spänningen i kretsarna ABD och BCD:

$(I_3 \cdot R_3) - (I_g \cdot R_g) - (I_1 \cdot R_1) = 0$

$(I_x \cdot R_x) - (I_2 \cdot R_2) + (I_g \cdot R_g) = 0$

Då kretsarna balanseras så att $I g = 0$ , så kan man omskriva den andra ekvationen till:

$I_3 \cdot R_3 = I_1 \cdot R_1$

$I_x \cdot R_x = I_2 \cdot R_2$

Då ekvationerna divideras med varandra och omformas, får man:

$R_x = {{R_2 \cdot I_2 \cdot I_3 \cdot R_3}\over{R_1 \cdot I_1 \cdot I_x}}$

Enligt den första lagen är $I 3 = I x$ och $I 1 = I 2$ . Det önskade värdet på $R x$ blir nu känt som:

$R_x = {{R_3 \cdot R_2}\over{R_1}}$

3: Om i stället alla fyra motstånd och spänningen ( $V s$ ) i spänningskällan är kända , kan spänningen ( $V$ ) över bryggan fås fram genom att bestämma spänningen över bägge spänningsdelarna och subtrahera dem från varandra. Ekvationen blir då:

$V = {{R_x}\over{R_3 + R_x}}V_s - {{R_2}\over{R_1 + R_2}}V_s$

Eller förenklat:

$V = \left({{R_x}\over{R_3 + R_x}} - {{R_2}\over{R_1 + R_2}}\right)V_s$

Tillämpningar

Eftersom det är betydligt enklare att avläsa en skala än att justera in ett nolläge, används i praktiken för det mesta metod två ovan. Matematiken integreras naturligtvis i en automatisk reglerkrets, så att resultatet står att avläsa direkt på en display, eller kopplat till ett centralt övervakningssystem.

Se även

Sensor

Denna artikel är till stora delar översatt från artikeln på engelskspråkiga Wikipedia

Wheatstones brygga

Från Rilpedia

Innehåll

Historia

Teori

Tillämpningar

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk