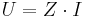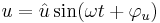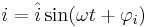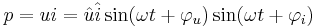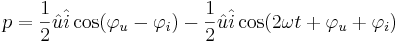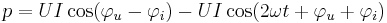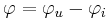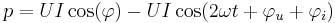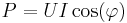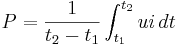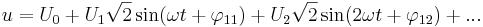Växelström

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Periodisk växelström

Icke-periodisk växelström. Skulle kunna vara utsignalen från en mikrofon

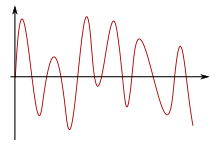
Växelström, AC (eng. alternating current), är en elektrisk ström vars riktning växlar. Om strömmen vid en viss tidpunkt har en viss riktning kommer den vid en senare tidpunkt att ha en motsatt riktning. Kraftverksproducerade växelströmmar och växelspänningar är periodiska och följer med tämligen stor noggrannhet en sinuskurva.

Framför allt är det möjligheten att transformera växelströmmen som gjort den till standard i de allmänna elnäten. Därigenom kan man enkelt åstadkomma en lämplig spänning för olika apparater och maskiner, samtidigt som kraftöverföringen sker med högspänningsledningar vilka ger relativt små överföringsförluster.

Innehåll

1 Historik
2 Allmän växelströmskrets
3 Effekt i växelströmskretsar
- 3.1 Effekt vid icke sinusformade spänningar och strömmar
4 Se även

Historik

Nikola Tesla tillskrivs upptäckten av växelström. Växelströmmen var dock känd långt innan Tesla började sitt arbete, men det var Tesla som gjorde växelströmmen användbar genom att konstruera den första växelströmsmotorn 1882 samt utvecklade transformatorn på ett sätt som möjliggjorde uppbyggnaden av dagens eldistributionsnät. Senare tillkom också konstruktionen av den mekaniskt enkla och robusta asynkronmotorn.

Allmän växelströmskrets

En passiv växelströmskrets (som inte innehåller transistorer, dioder eller andra "aktiva" element) kan abstraheras till en tvåpol med konstanta egenskaper, en komponent med enbart två anslutningsklämmor. Beroende på dess uppbyggnad kommer tvåpolen att ha en kapacitiv eller induktiv karaktär, vilket bestämmer kretsens fasvridande förmåga och hur den behandlar mottagen effekt. De fasvridande egenskaperna behandlas i

En induktiv eller kapacitiv tvåpol har en energilagrande förmåga. Energi lagras i elektromagnetiska fält (laddningskonfigurationer) under en del av växelströmsperioden. Denna effektdel, som kallas reaktiv effekt, kommer att sändas tillbaka till växeleffektkällan under en annan del av växelströmsperioden.

Förhållandet mellan växelspänning och växelström för en passiv tvåpol är enligt Ohms lag

$\ U = Z\cdot I$

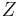där $\ Z$ är kretsens impedans, vilken i det allmänna fallet är sammansatt av resistans och reaktans.

Effekt i växelströmskretsar

Motoriskt referensval (effekt tillförs tvåpolen) för en tvåpols momentaneffekt

Den utvecklade momentan- och medeleffekten för en växelströmskrets. Strömmen och spänningen är inbördes fasförskjutna. Notera att effekten kan vara både positiv (mottagen) och negativ (avgiven)

Vid undersökning av effektförhållanden i växelströmskretsar är det viktigt att skilja mellan momentaneffekt och medeleffekt.

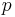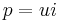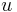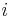Momentaneffekten symboliseras $\ p$ och är definitionsmässigt $\ p = ui$ , det vill säga produkten av spänningens och strömmens momentanvärden. Eftersom i det allmänna fallet både $\ u$ och $\ i$ varierar kommer också 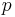$\ p$ att variera med tiden. För att bestämmandet av momentaneffekten skall bli entydigt och meningsfullt räcker det inte med att konstatera att 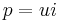$\ p = ui$ utan det är också nödvändigt att konstatera huruvida $\ p$ står för mottagen eller avgiven effekt. Låt oss utgå från tvåpolen i vidstående figur med motoriskt referensval, vilket innebär att momentaneffekten referensmässigt står för mottagen effekt sett från tvåpolen. Huruvida effekten också är fysikaliskt mottagen eller fysikaliskt avgiven beror på $\ p$ 's tecken.

Låt oss anta en sinusformad karaktär hos både spänning och ström:

$\ u = \hat u \sin(\omega t + \varphi _u)$

$\ i = \hat i \sin(\omega t + \varphi _i)$

Den mottagna effekten kan då skrivas

$\ p = ui = \hat u \hat i\sin(\omega t + \varphi _u)\sin(\omega t + \varphi _i)$

vilket kan skrivas om till

$\ p = {1 \over 2}\hat u \hat i \cos(\varphi _u - \varphi _i) - {1 \over 2}\hat u \hat i \cos(2\omega t + \varphi _u + \varphi _i)$

eller med användande av effektivvärdessymboler

$\ p = UI \cos(\varphi _u - \varphi _i) - UI \cos(2\omega t + \varphi _u + \varphi _i)$

Om vi definierar

$\ \varphi = \varphi _u - \varphi _i$

kan vi skriva

$\ p = UI \cos(\varphi) - UI \cos(2\omega t + \varphi _u + \varphi _i)$

Den momentana effekten kan således anses bestå av två delar nämligen

En konstant del 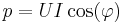$\ p = UI \cos(\varphi)$ som om 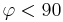$\ \varphi < 90$ grader (motsvarar en passiv tvåpol) alltid är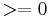 $\ >= 0$

En med dubbla frekvensen varierande del 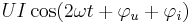$UI \cos(2\omega t + \varphi _u + \varphi _i)$ vars amplitud är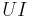 $\ UI$

Den av tvåpolen förbrukade effekten (medeleffekten) är den konstanta delen

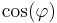$\ P = UI \cos(\varphi)$

Faktorn $\ \cos(\varphi)$ spelar en mycket viktig roll vid sinusformigt varierande spänning och ström. Den har fått en särskild benämning: effektfaktorn. Dess värde beror på tvåpolens uppbyggnad eftersom denna är avgörande för 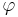$\ \varphi$ 's belopp och tecken.

Om 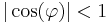$\ |\cos(\varphi)| < 1$ förekommer reaktiv effekt. Över en period är summan av de reaktiva effektbidragen noll. Den reaktiva effekten endast mottages och avges och förbrukas således inte av tvåpolen.

Effekt vid icke sinusformade spänningar och strömmar

Medeleffekten definieras som

$P = {1 \over t_2 - t_1}\int_{t_1}^{t_2} ui\,dt$

Om tvåpolens spänning och ström antas vara fourieruppdelade kan medeleffekten erhållas uttryckt i fourierkomponenterna. Vi utgår från

$\ u = U_0 + U_1 \sqrt{2}\sin(\omega t + \varphi _{11}) + U_2 \sqrt{2}\sin(2\omega t + \varphi _{12}) + ...$

$\ i = I_0 + I_1 \sqrt{2}\sin(\omega t + \varphi _{21}) + I_2 \sqrt{2}\sin(2\omega t + \varphi _{22}) + ...$

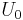Där $\ U_0$ är likspänningskomponenten och 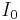$\ I_0$ är likströmskomponenten. Efter multiplikation och termvis integrering erhålls

$\ P = U_0 I_0 + U_1 I_1 \cos(\varphi _1) + U_2 I_2 \cos(\varphi _2) + U_3 I_3 \cos(\varphi _3) + ...$

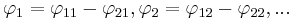där $\ \varphi _1 = \varphi _{11} - \varphi _{21}, \varphi _2 = \varphi _{12} - \varphi _{22}, ...$ .

Detta kan uttryckas som:

Endast termer med samma frekvenskomponenter (samma multipler av 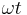$\ \omega t$ ) ger bidrag till medeleffekten.

Resultatet innebär att om exempelvis en sinusformad spänning påtrycks en ickelinjär tvåpol med en icke sinusformad ström som följd så kommer vid beräkningen av tvåpolens medeleffekt endast strömmens grundton (som har samma frekvens som spänningen) att ha betydelse.

Se även

Växelström

Från Rilpedia

Innehåll

Historik

Allmän växelströmskrets

Effekt i växelströmskretsar

Effekt vid icke sinusformade spänningar och strömmar

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk