Weierstrassfunktionen

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Weiserstrassfunktionen i intervallet [-2,2]. Det inzoomade området visar att funktionen är en fraktal.

Weierstrassfunktionen skapades av den tyske matematikern Karl Weierstrass under sin tid som professor i Berlin ^[1]. Den är ett exempel på att en överallt kontinuerlig funktion inte behöver vara deriverbar någonstans och har formen

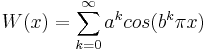
$W(x)= \sum_{k=0}^\infty a^k cos(b^k \pi x)$

där 0<a<1 , 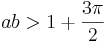$ab>1+\frac{3 \pi}{2}$ och b är ett udda heltal större än 1 ^[2].

Historia

Historiskt sett ligger Weierstrassfunktionens betydelse i att den var den första publicerade funktion som motsade att alla kontinuerliga funktioner är deriverbara överallt utom i ett visst antal diskreta punkter. Det hade dock skapats funktioner med dessa egenskaper tidigare, dock publicerades dessa aldrig vilket gjorde att de inte fick samma spridning som Weierstrassfunktionen. ^[2]. Weierstrassfunktionen anses också vara en av de första fraktalerna som skapats.

Bevis av kontinuitet

Eftersom

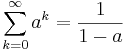
$\sum_{k=0}^\infty a^k = \frac{1}{1-a}$

och

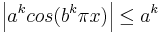
$\left| a^k cos(b^k \pi x) \right| \le a^k$

kommer funktionen vara kontinuerlig på hela 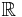$\mathbb{R}$ enligt Weierstrass majorantsats ^[2].

Bevis av icke-deriverbarhet

Bevisidé

Beviset, utförd enligt ^[2], bygger på att man ska bevisa att höger- och vänsterderivaten är olika, dvs att 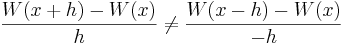$\frac{W(x+h)-W(x)}{h} \ne \frac{W(x-h)-W(x)}{-h}$

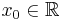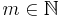Börja med att låta $x_0 \in \mathbb{R}$ och $m \in \mathbb{N}$ var två godtyckliga tal.

Välj 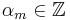$\alpha_m \in \mathbb{Z}$ så att $b^m x_0 - \alpha \in \left( -\frac{1}{2}, \frac{1}{2} \right]$

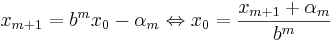
och sätt $x_{m+1}=b^m x_0 - \alpha_m \Leftrightarrow x_0= \frac{x_{m+1}+\alpha_m}{b^m}$

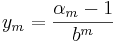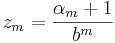$y_m = \frac{\alpha_m -1}{b^m}$ och $z_m = \frac{\alpha_m +1}{b^m}$ .

För att visa att $y m < x 0 < z m$ görs följande beräkningar:

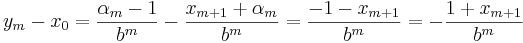
$y_m-x_0 = \frac{\alpha_m -1}{b^m} - \frac{x_{m+1}+\alpha_m}{b^m} = \frac{-1-x_{m+1}}{b^m} = -\frac{1+x_{m+1}}{b^m}$

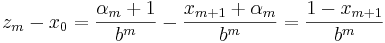
$z_m-x_0 = \frac{\alpha_m +1}{b^m} - \frac{x_{m+1}+\alpha_m}{b^m} = \frac{1-x_{m+1}}{b^m}$

vilket ger olikheten

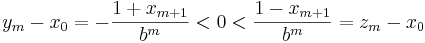
$y_m - x_0 = -\frac{1+x_{m+1}}{b^m} < 0 < \frac{1-x_{m+1}}{b^m} = z_m-x_0$

varför $y m < x 0 < z m$ .

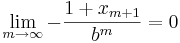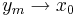Samtidigt fås att $\lim_{m \to \infty}{-\frac{1+x_{m+1}}{b^m}} = 0$ , dvs $y_m \to x_0$ från vänster då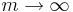 $m \to \infty$

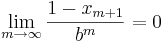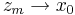och $\lim_{m \to \infty}{\frac{1-x_{m+1}}{b^m}} = 0$ , dvs $z_m \to x_0$ från höger då 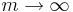$m \to \infty$ efter b>1.

Uppskattning av vänsterderivatan

Den vänsterderivatan begrundas först och delas upp i $S 1$ och $S 2$ enligt

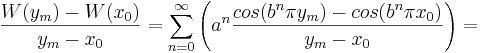
$\frac{W(y_m)-W(x_0)}{y_m-x_0} = \sum_{n=0}^\infty \left( a^n \frac{cos(b^n \pi y_m) - cos(b^n \pi x_0)} {y_m - x_0} \right) =$

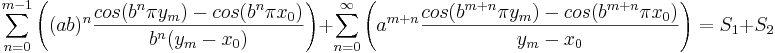$\sum_{n=0}^{m-1} \left( (ab)^n \frac{cos(b^n \pi y_m) - cos(b^n \pi x_0)} {b^n(y_m - x_0)} \right) + \sum_{n=0}^\infty \left( a^{m+n} \frac{cos(b^{m+n} \pi y_m) - cos(b^{m+n} \pi x_0)} {y_m - x_0} \right) = S_1 + S_2$ .

Där alltså S1 är summan av kvoterna från n=0 till n=m-1 och S2 är summan av kvoterna från n=m till oändligheten. S1 och S2 behandlas sedan var för sig för kunna uppskatta S1 uppåt och S2 nedåt.

Uppskattning av S1

S1 skrivs om med hjälp av den trigonometriska formeln 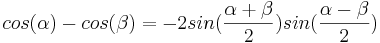$cos(\alpha)-cos(\beta) = -2sin(\frac{\alpha+\beta}{2})sin(\frac{\alpha-\beta}{2})$

samt det faktum att 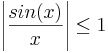$\left| \frac{sin(x)}{x}\right| \le 1$ .

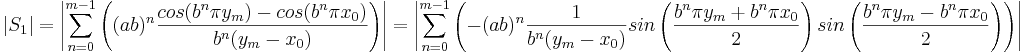
$\left| S_1 \right| = \left| \sum_{n=0}^{m-1} \left( (ab)^n \frac{cos(b^n \pi y_m) - cos(b^n \pi x_0)} {b^n(y_m - x_0)} \right) \right| = \left| \sum_{n=0}^{m-1} \left( -(ab)^n \frac{1}{b^n (y_m - x_0)} sin \left( \frac{b^n \pi y_m + b^n \pi x_0}{2} \right) sin \left( \frac{b^n \pi y_m - b^n \pi x_0}{2} \right) \right) \right|$

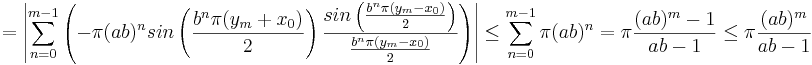
$= \left| \sum_{n=0}^{m-1} \left( - \pi (ab)^n sin \left( \frac{b^n \pi (y_m + x_0)}{2} \right) \frac{sin \left( \frac{b^n \pi (y_m - x_0)}{2} \right)}{\frac{b^n \pi (y_m - x_0)}{2}} \right) \right| \le \sum_{n=0}^{m-1} \pi (ab)^n = \pi \frac{(ab)^m - 1}{ab-1} \le \pi \frac{(ab)^m}{ab-1}$

Uppskattning av S2

S2 kan, då b är ett udda heltal och 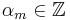$\alpha_m \in \mathbb{Z}$ skrivas om enligt

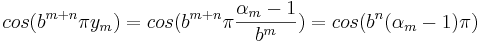
$cos(b^{m+n} \pi y_m) = cos(b^{m+n} \pi \frac{\alpha_m -1}{b^m}) = cos( b^n (\alpha_m - 1) \pi)$

och

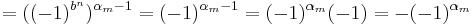
$= ((-1)^{b^n})^{\alpha_m -1} = (-1)^{\alpha_m -1} = (-1)^{\alpha_m} (-1) = - (-1)^{\alpha_m}$

vilket ger

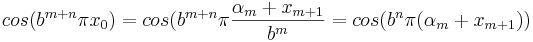
$cos(b^{m+n} \pi x_0) = cos(b^{m+n} \pi \frac{\alpha_m + x_{m+1}}{b^m}=cos(b^n \pi (\alpha_m + x_{m+1}))$

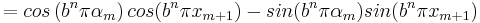
$= cos\left(b^n \pi \alpha_m \right) cos(b^n \pi x_{m+1}) - sin(b^n \pi \alpha_m) sin(b^n \pi x_{m+1})$

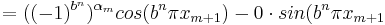
$=((-1)^{b^n})^{\alpha_m} cos(b^n \pi x_{m+1}) - 0 \cdot sin(b^n \pi x_{m+1}$

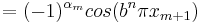$=(-1)^{\alpha_m} cos(b^n \pi x_{m+1})$ .

Vi får alltså att

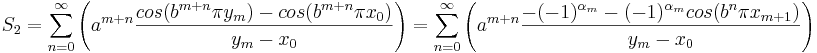
$S_2 = \sum_{n=0}^\infty \left( a^{m+n} \frac{cos(b^{m+n} \pi y_m) - cos(b^{m+n} \pi x_0)} {y_m - x_0} \right) = \sum_{n=0}^\infty \left( a^{m+n} \frac{-(-1)^{\alpha_m} - (-1)^{\alpha_m} cos(b^n \pi x_{m+1})}{y_m - x_0} \right)$

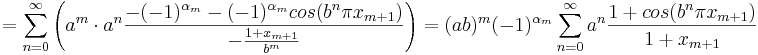$= \sum_{n=0}^\infty \left( a^m \cdot a^n \frac{-(-1)^{\alpha_m} - (-1)^{\alpha_m} cos(b^n \pi x_{m+1})}{-\frac{1+x_{m+1}}{b^m}} \right) =(ab)^m (-1)^{\alpha_m} \sum_{n=0}^\infty a^n \frac{1+cos(b^n \pi x_{m+1})}{1+x_{m+1}}$ .

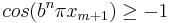
I och med att $x_{m+1} \in \left( -\frac{1}{2}, \frac{1}{2} \right]$ och $cos(b^n \pi x_{m+1}) \ge -1$

är alla termer positiva vilket ger att

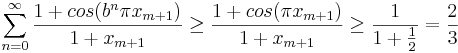$\sum_{n=0}^\infty \frac{1+cos(b^n \pi x_{m+1})}{1+x_{m+1}} \ge \frac{1+cos(\pi x_{m+1})}{1+x_{m+1}} \ge \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}$ .

Resultat

Uppskattningarna av S1 och S2 ger att det existerar ett $\epsilon_1 \in \left[ -1,1 \right]$ och $η 1 > 1$ så att

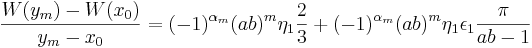
$\frac{W(y_m) - W(x_0)}{y_m - x_0} = (-1)^{\alpha_m} (ab)^m \eta_1 \frac{2}{3} + (-1)^{\alpha_m} (ab)^m \eta_1 \epsilon_1 \frac{\pi}{ab-1}$

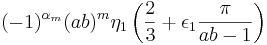$(-1)^{\alpha_m} (ab)^m \eta_1 \left( \frac{2}{3} + \epsilon_1 \frac{\pi}{ab-1} \right)$ .

Uppskattning av högerderivatan

Högerderivatan uppskattas på samma sätt som den vänstra enligt

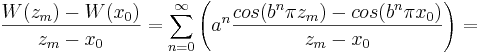
$\frac{W(z_m)-W(x_0)}{z_m-x_0} = \sum_{n=0}^\infty \left( a^n \frac{cos(b^n \pi z_m) - cos(b^n \pi x_0)} {z_m - x_0} \right) =$

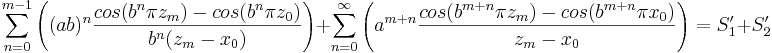$\sum_{n=0}^{m-1} \left( (ab)^n \frac{cos(b^n \pi z_m) - cos(b^n \pi z_0)} {b^n(z_m - x_0)} \right) + \sum_{n=0}^\infty \left( a^{m+n} \frac{cos(b^{m+n} \pi z_m) - cos(b^{m+n} \pi x_0)} {z_m - x_0} \right) = S'_1 + S'_2$ .

Uppskattning av S'1

$S' 1$ skrivs om på samma sätt som $S 1$ .

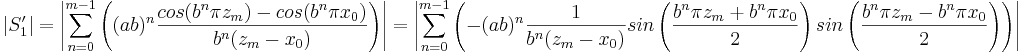
$\left| S'_1 \right| = \left| \sum_{n=0}^{m-1} \left( (ab)^n \frac{cos(b^n \pi z_m) - cos(b^n \pi x_0)} {b^n(z_m - x_0)} \right) \right| = \left| \sum_{n=0}^{m-1} \left( -(ab)^n \frac{1}{b^n (z_m - x_0)} sin \left( \frac{b^n \pi z_m + b^n \pi x_0}{2} \right) sin \left( \frac{b^n \pi z_m - b^n \pi x_0}{2} \right) \right) \right|$

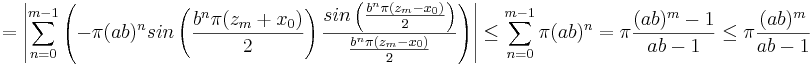
$= \left| \sum_{n=0}^{m-1} \left( - \pi (ab)^n sin \left( \frac{b^n \pi (z_m + x_0)}{2} \right) \frac{sin \left( \frac{b^n \pi (z_m - x_0)}{2} \right)}{\frac{b^n \pi (z_m - x_0)}{2}} \right) \right| \le \sum_{n=0}^{m-1} \pi (ab)^n = \pi \frac{(ab)^m - 1}{ab-1} \le \pi \frac{(ab)^m}{ab-1}$

Uppskattning av S'2

$S' 2$ kan uppskattas på samma sätt som $S 2$ enligt nedan.

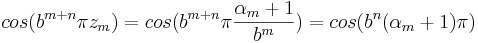
$cos(b^{m+n} \pi z_m) = cos(b^{m+n} \pi \frac{\alpha_m + 1}{b^m}) = cos( b^n (\alpha_m + 1) \pi)$

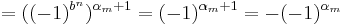
$= ((-1)^{b^n})^{\alpha_m + 1} = (-1)^{\alpha_m + 1} = - (-1)^{\alpha_m}$

Från beräkningen av S2 fås även att

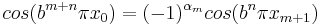
$cos(b^{m+n} \pi x_0) = (-1)^{\alpha_m} cos(b^n \pi x_{m+1})$

vilket ger att

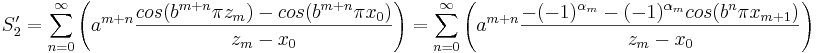
$S'_2 = \sum_{n=0}^\infty \left( a^{m+n} \frac{cos(b^{m+n} \pi z_m) - cos(b^{m+n} \pi x_0)} {z_m - x_0} \right) = \sum_{n=0}^\infty \left( a^{m+n} \frac{-(-1)^{\alpha_m} - (-1)^{\alpha_m} cos(b^n \pi x_{m+1})}{z_m - x_0} \right)$

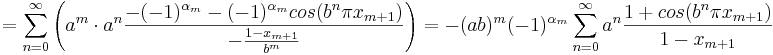$= \sum_{n=0}^\infty \left( a^m \cdot a^n \frac{-(-1)^{\alpha_m} - (-1)^{\alpha_m} cos(b^n \pi x_{m+1})}{-\frac{1-x_{m+1}}{b^m}} \right) =-(ab)^m (-1)^{\alpha_m} \sum_{n=0}^\infty a^n \frac{1+cos(b^n \pi x_{m+1})}{1-x_{m+1}}$ .

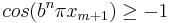
I och med att $x_{m+1} \in \left( -\frac{1}{2}, \frac{1}{2} \right]$ och $cos(b^n \pi x_{m+1}) \ge -1$

är alla termer positiva vilket ger att

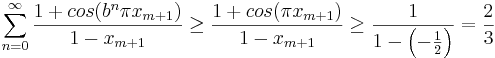$\sum_{n=0}^\infty \frac{1+cos(b^n \pi x_{m+1})}{1-x_{m+1}} \ge \frac{1+cos( \pi x_{m+1})}{1-x_{m+1}} \ge \frac{1}{1 - \left(-\frac{1}{2} \right)} = \frac{2}{3}$ .

Resultat

Uppskattningarna av S'1 och S'2 ger att det existerar ett $\epsilon_1 \in \left[ -1,1 \right]$ och $η 1 > 1$ så att

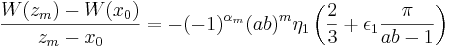
$\frac{W(z_m) - W(x_0)}{z_m - x_0} = -(-1)^{\alpha_m} (ab)^m \eta_1 \left( \frac{2}{3} + \epsilon_1 \frac{\pi}{ab-1} \right)$

Slutsats

Vänster- och högerderivatan kan skrivas enligt:

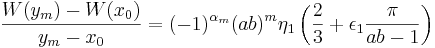
$\frac{W(y_m) - W(x_0)}{y_m - x_0} = (-1)^{\alpha_m} (ab)^m \eta_1 \left( \frac{2}{3} + \epsilon_1 \frac{\pi}{ab-1} \right)$

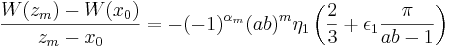
$\frac{W(z_m) - W(x_0)}{z_m - x_0} = -(-1)^{\alpha_m} (ab)^m \eta_1 \left( \frac{2}{3} + \epsilon_1 \frac{\pi}{ab-1} \right)$

Detta tillsammans med att

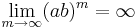
$\lim_{m \to \infty}(ab)^m = \infty$

ger direkt att funktionen saknar derivata eftersom vänster- och högerderivatan har olika tecken.

Fotnoter

↑ Jan Thompson & Thomas Martinsson: Matematiklexikon, 1991. ISBN 91-46-16515-0.
↑ ^2,0 ^2,1 ^2,2 ^2,3 http://epubl.luth.se/1402-1617/2003/320/LTU-EX-03320-SE.pdf

[0] Jan Thompson & Thomas Martinsson: Matematiklexikon, 1991. ISBN 91-46-16515-0.

[lule.C3.A5uni-1] 2,0 ^2,1 ^2,2 ^2,3 http://epubl.luth.se/1402-1617/2003/320/LTU-EX-03320-SE.pdf

[1]

[2]

Weierstrassfunktionen

Från Rilpedia

Innehåll

Historia

Bevis av kontinuitet

Bevis av icke-deriverbarhet

Bevisidé

Uppskattning av vänsterderivatan

Uppskattning av S1

Uppskattning av S2

Resultat

Uppskattning av högerderivatan

Uppskattning av S'1

Uppskattning av S'2

Resultat

Slutsats

Fotnoter

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk